Question

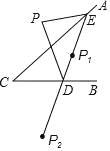
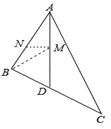
【题目】如图，在△ABC中，AD平分∠BAC交BC于点D，点M，N分别是AD和AB上的动点，当S△ABC＝12，AC＝8时，BM+MN的最小值等于_____．

Answer 1

【答案】3

【解析】

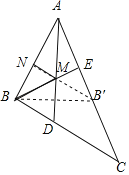
作点B关于AD的对称点B′,过点B′作B′N⊥AB于N交AD于M，由轴对称确定最短路线问题，点M即为使BM+MN最小的点，算出B′N即可

解：如图，作点B关于AD的对称点B′

∵AD是∠BAC的平分线，

∴点B关于AD的对称点B′在AC上，

过点B′作B′N⊥AB于N交AD于M，

由轴对称确定最短路线问题，点M即为使BM+MN最小的点，B′N＝BM+MN，

过点B作BE⊥AC于E，

∵AC＝8，S△ABC＝20，

∴×8BE＝12，

解得BE＝3，

∵AD是∠BAC的平分线，B′与B关于AD对称，

∴AB＝AB′，

∴△ABB′是等腰三角形，

∴B′N＝BE＝3，

即BM+MN的最小值是3．

故答案为：3．