Question

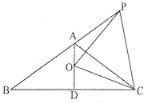
【题目】已知：如图，在△ABC中，∠ABC的平分线BP与AC边的垂直平分线PQ交于点P，过点P分别作PD⊥AB于点D，PE⊥BC于点E，若BE＝10cm，AB＝6cm，求CE的长．

Answer 1

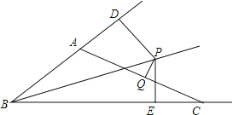
【答案】4cm．

【解析】

连接AP，CP，根据角平分线性质求出PD=PE，根据线段垂直平分线求出PA=PC，根据HL证RT△PAD≌RT△PCE，即可得出答案．

解：如图，连接AP、CP，

∵BP平分∠ABC，PD⊥AB，PE⊥BC，

∴∠PBD＝∠PBE，∠PDB＝∠PEC＝90°，PD＝PE，

在△BPD和△BPE中，

，

∴△BPD≌△BPE（AAS），

∴BD＝BE，

又∵BE＝10cm，AB＝6cm，

∴AD＝BD﹣AB＝BE﹣AB＝4cm，

∵PQ垂直平分AC，

∴PA＝PC，

在RT△PAD和RT△PCE中，

，

∴RT△PAD≌RT△PCE（HL），

∴CE＝AD＝4cm．