Question

【题目】已知在平面直角坐标系中，点的坐标是，点是第一象限内一动点。

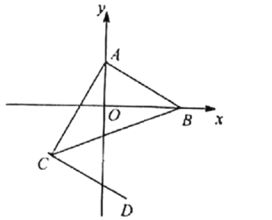
(1) ①：如图①.若动点满足，且，求点的坐标。

②：如图②，在第(1)问的条件下，将逆时针旋转至如图所示位置，求的值.

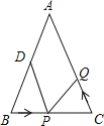
(2)如图③，若点与点关于轴对称，且， 若动点满足'，问：的值是否发生变化？若变化，请说明理由，若不变化，请求出其值。

Answer 1

【答案】（1）①（4,0）；②6；（2）的值不变，为2.

【解析】

（1）利用绝对值和偶次方的非负性求出点P坐标，再作辅助线利用三角形全等即可求得点B坐标.

（2）利用三角形全等，即可求出.

（3）利用三角形全等，求得，再利用线段之间的关系，即可求出.

（1）①∵满足

∴ ∴

∴P（3,3）如图所示，PM=PN

∵ ∴

∴

∴NB=AM

AM=MO-AO=3-2=1

∴B（4,0）

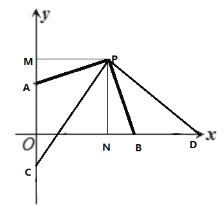
② 如图所示，由①可证得

∴BD=AC，设BD=AC=a

则OD=4+a，OC=AC-AO=a-2

OD-OC=4+a-( a-2)=6

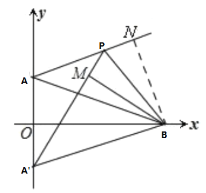
（2）过点B作BN⊥AP于点N

又∵⊥

∴

∵点与点关于轴对称

∴

又∵

∴

∴

∴

∴

∴的值不变，为2.