题目内容
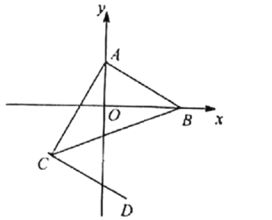
【题目】已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)
(1)求该函数的关系式;
(2)求该函数图象与坐标轴的交点坐标;
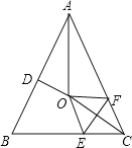
(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.
【解析】
(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B点坐标代入,即可求出二次函数的解析式;
(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;
(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.
(1)设抛物线顶点式y=a(x+1)2+4,
将B(2,﹣5)代入得:a=﹣1,
∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;
(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),
令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,
即抛物线与x轴的交点为:(﹣3,0),(1,0);
(3)设抛物线与x轴的交点为M、N(M在N的左侧),
由(2)知:M(﹣3,0),N(1,0),
当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,
故A'(2,4),B'(5,﹣5),
∴S△OA′B′=![]() ×(2+5)×9﹣
×(2+5)×9﹣![]() ×2×4﹣
×2×4﹣![]() ×5×5=15.
×5×5=15.
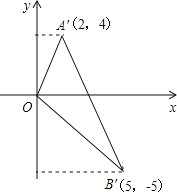

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 |
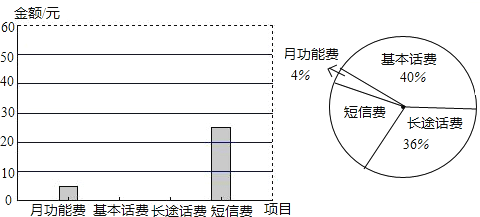
(1)该月小王手机话费共有多少元?
(2)扇形统计图中,表示短信费的扇形的圆心角为多少度?
(3)请将表格补充完整;
(4)请将条形统计图补充完整.