Question

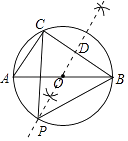
【题目】已知：如图，已知⊙O是△ABC的外接圆，AB为⊙O的直径，AC=6cm，BC=8cm．
（1）求⊙O的半径；
（2）请用尺规作图作出点P，使得点P在优弧CAB上时，△PBC的面积最大，请保留作图痕迹，并求出△PBC面积的最大值．

Answer 1

【答案】
（1）解：∵AB为⊙O的直径，

∴∠C=90°，

在Rt△ABC中，∵AC=6，BC=8，

∴AB= =10，

∴⊙O的半径为5cm

（2）解：如图，作BC的垂直平分线交优弧CAB于P，交BC于D，

则BD=CD= BC=4，

在Rt△OBD中，OD= =3，

∴PD=3+5=8，

S△PBC= PDBC= ×8×8=32．

【解析】（1）利用圆周角定理得到∠C=90°，则利用勾股定理可计算出AB=10，从而得到⊙O的半径；（2）如图，作BC的垂直平分线交优弧CAB于P，交BC于D，利用垂径定理得到BD=CD= BC=4，则利用勾股定理可计算出OD=3，然后利用三角形面积公式计算此时△PBC的面积．
【考点精析】关于本题考查的三角形的外接圆与外心，需要了解过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心才能得出正确答案．