题目内容
【题目】如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=﹣ ![]() (x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(1)当m=2时,k= , b=;当m=﹣1时,k= , b=;
(2)根据(1)中的结果,用含m的代数式分别表示k与b,并证明你的结论;
(3)当正方形ABCD的顶点C落在抛物线的对称轴上时,求对应的抛物线的函数关系式;
(4)当正方形ABCD的顶点D落在抛物线上时,直接写出对应的直线y=kx+b的函数关系式.
【答案】
(1)![]() ;1;
;1;![]() ;﹣2
;﹣2
(2)
解:k= ![]() ,b=m﹣1.
,b=m﹣1.
证明:∵y=﹣ ![]() (x﹣2)2+m,
(x﹣2)2+m,
∴抛物线的顶点坐标为(2,m).
把x=0代入得:y=m﹣1.
∴b=m﹣1.
设直线AB的解析式为y=kx+m﹣1.
将x=2,y=m代入得:2k+m﹣1=m,解得k= ![]()
(3)
解:如图1所示,过点C作CE⊥y轴,垂足为E.
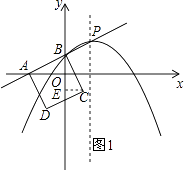
∵ABCD为正方形,
∴AB=BC,∠ABE+∠EBC=90°.
又∵∠ABO+∠BAO=90°,
∴∠BAO=∠EBC.
在△ABO和△BCE中  ,
,
∴△ABO≌△BCE.
∴EC=OB=2.
∴m﹣1=2.
∴m=3.
∴抛物线的解析式为y=﹣ ![]() (x﹣2)2+3
(x﹣2)2+3
(4)
解:如图2所示当点B在y轴的正半轴上时,过点D作DE⊥x轴与点E.

由(2)可知:直线AB的解析式为y= ![]() x+m﹣1.
x+m﹣1.
当x=0时,y=m﹣1,当y=0时,x=2﹣2m.
∴OA=2m﹣2,OB=m﹣1.
∵∠BAO+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAO=∠ADE.
在△ABO和△DAE中  ,
,
∴△ABO≌△DAE.
∴AE=OB=1﹣m,ED=AO=2m﹣2.
∴D(1﹣m,2﹣2m).
∵点D在抛物线上,
∴2﹣2m=﹣ ![]() (﹣m﹣1)2+m,解得m=9或m=1(舍去).
(﹣m﹣1)2+m,解得m=9或m=1(舍去).
∴直线的解析式为y= ![]() x+9.
x+9.
如图3所示:当点B在y轴的负半轴上时,

当x=0时,y=m﹣1,当y=0时,x=2﹣2m.
∴OA=2﹣2m,OB=1﹣m.
∵∠BAO+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAO=∠ADE.
在△ABO和△DAE中  ,
,
∴△ABO≌△DAE.
∴AE=OB,ED=AO.
∴D(3﹣3m,2m﹣2).
∵点D在抛物线上,
∴2m﹣2=﹣ ![]() (1﹣3m)2+m,解得m=﹣
(1﹣3m)2+m,解得m=﹣ ![]() 或m=1(舍去).
或m=1(舍去).
∴直线的解析式为y= ![]() x﹣
x﹣ ![]() .
.
综上所述,直线的解析式为y= ![]() x+9或y=
x+9或y= ![]() x﹣
x﹣ ![]()
【解析】解:(1)当m=2时,y=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
∴P(2,2).
把x=0代入得:y=1,
∴B(0,1).
设直线AB的解析式为y=kx+1,
将点P的坐标(2,2)代入得:2k+1=2,解得:k= ![]() .
.
∴k= ![]() ,b=1.
,b=1.
当m=﹣1时,y=﹣ ![]() (x﹣2)2﹣1.
(x﹣2)2﹣1.
∴P(2,﹣1).
把x=0代入得:y=﹣2,
∴B(0,﹣2).
设直线AB的解析式为y=kx﹣2,
将点P的坐标(2,﹣1)代入得:2k﹣2=﹣1,解得:k= ![]() .
.
∴k= ![]() ,b=﹣2.
,b=﹣2.
所以答案是: ![]() ;1;
;1; ![]() ;﹣2.
;﹣2.
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |
(1)根据上述统计图可得此次采访的人数为人,m= , n=;
(2)根据以上信息补全条形统计图; 
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.




