题目内容
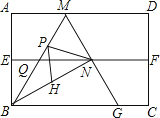
【题目】如图(1),在矩形ABCD中,AB=4,BC=3,点E是射线CD上的一个动点,把△BCE沿BE折叠,点C的对应点为F.
(1)若点F刚好落在线段AD的垂直平分线上时,求线段CE的长;
(2)若点F刚好落在线段AB的垂直平分线上时,求线段CE的长;
(3)当射线AF交线段CD于点G时,请直接写出CG的最大值.
【答案】
(1)
解:如图1中,MN是线段AD的中垂线,作FH⊥CD于H.
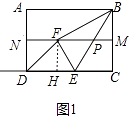
在Rt△BFM中,∵BF=BC=3,BM= ![]() ,
,
∴FM=CH= ![]() =
= ![]() ,设CE=EF=x,
,设CE=EF=x,
在Rt△EFH中,∵EF2=FH2+HE2,
∴x2=( ![]() )2+(
)2+( ![]() ﹣x)2,
﹣x)2,
∴x= ![]() ,
,
∴CE= ![]()
(2)
解:如图2中,MN是线段AB的中垂线,设EF=CE=x.
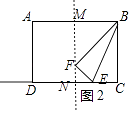
在Rt△BFM中,∵∠BMF=90°,BM=2,BF=BC=3,
∴MF= ![]() =
= ![]() ,
,
∵MN=BC=3,
∴FN=3﹣ ![]() ,EN=2﹣x,
,EN=2﹣x,
在Rt△EFN中,∵EF2=FN2+NE2,
∴x2=(3﹣ ![]() )2+(2﹣x)2,
)2+(2﹣x)2,
∴x= ![]()
(3)
解:如图3中,
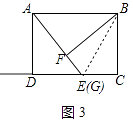
欲求CG的最大值,只要求出DG的最小值即可,
∵DG=ADtan∠GAD,
∴∠GAD最小时,DG的值最小,
∵BF=BC,BF是定值,
∴当BF⊥AG时,∠BAF的值最大,即∠DAG的值最小,
当BF⊥AG时,易知点E与点G共点,
设CG=GF=x,
在Rt△ABF中,∵∠AFB=90°,AB=4,BF=BC=3,
∴AF= ![]() =
= ![]() ,
,
在Rt△ADE中,∵AD2+DG2=AG2,
∴32+(4﹣x)2=( ![]() +x)2,
+x)2,
∴x=4﹣ ![]() .
.
∴CG的最大值为4﹣ ![]() ,
,
故答案为4﹣ ![]()
【解析】(1)如图1中,MN是线段AD的中垂线,作FH⊥CD于H.设CE=EF=x,在Rt△EFH中,根据EF2=FH2+HE2 , 构建方程即可解决问题.(2)如图2中,MN是线段AB的中垂线,设EF=CE=x.在Rt△EFN中,根据EF2=FN2+NE2 , 构建方程即可解决题.(3)欲求CG的最大值,只要求出DG的最小值即可,由DG=ADtan∠GAD,推出∠GAD最小时,DG的值最小,由BF=BC,BF是定值,推出当BF⊥AG时,∠BAF的值最大,即∠DAG的值最小,当BF⊥AG时,易知点E与点G共点,设CG=GF=x,在Rt△ADE中,根据AD2+DG2=AG2 , 构建方程即可解决问题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表. 
等级 | 得分x(分) | 频数(人) |
A | 95≤x≤100 | 4 |
B | 90≤x<95 | m |
C | 85≤x<90 | n |
D | 80≤x<85 | 24 |
E | 75≤x<80 | 8 |
F | 70≤x<75 | 4 |
请根据图表提供的信息,解答下列问题:
(1)本次抽样调查样本容量为 , 表中:m= , n=;扇形统计图中,E等级对应扇形的圆心角α等于度;
(2)该校决定从本次抽取的A等级学生(记为甲、乙、病、丁)中,随机选择2名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.