Question

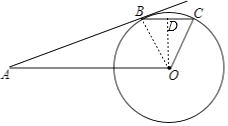
【题目】如图，AB切⊙O于点B，OA=6，sinA= ，弦BC∥OA．
（1）求AB的长；
（2）求四边形AOCB的面积．

Answer 1

【答案】
（1）解：连接OB，如图，

∵AB切⊙O于点B，

∴OB⊥AB，

∴∠ABO=90°，

∴sinA= = ，

∴OB= ×6=2，

∴AB= =4

（2）解：作OD⊥BC于D，如图，则BD=CD，

∵BC∥OA，

∴∠AOB=∠OBD，

∴∠BOD=∠A，

∴sin∠BOD= = ，

∴BD= ×2= ，

∴BC=2BD= ，OD= = ，

∴四边形AOCB的面积=S△AOB+S△BOC= ×2×4 + × × = ．

【解析】（1）连接OB，如图，利用切线的性质得∠ABO=90°，再利用∠A的正弦可计算出OB，然后利用勾股定理可计算出AB；（2）作OD⊥BC于D，如图，利用垂径定理得到BD=CD，再利用平行线的性质和互余得到∠BOD=∠A，则根据∠BOD的正弦可求出BD，然后利用勾股定理计算出OD，最后利用三角形面积公式计算四边形AOCB的面积．
【考点精析】关于本题考查的切线的性质定理和解直角三角形，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能得出正确答案．