题目内容
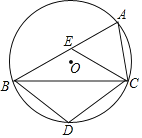
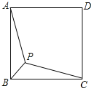
【题目】如图，点
是正方形
内一点，连接
、
、
，若
，
，
，则正方形的边长为________．
【答案】
【解析】
将△ABP绕点B沿顺时针方向旋转90°到△BCQ的位置，连接PQ；先求出PQ的长，再求出∠PQC=90°，利用勾股定理求出QC的长，最后利用勾股定理求出BC的长．
如图,将△ABP绕点B沿顺时针方向旋转90°，
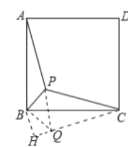
到△BCQ的位置，连接PQ；
则BQ=BP=
,∠BQC=∠BPA=135°，
则△PBQ是等腰直角三角形，
即PQ=
，
故∠BQP=∠BPQ=45°,∠PQC=135°45°=90°；
由勾股定理得：QC2=PC2PQ2,，CQ=2
在△BQC中,∠BQC=135°,BQ=,CQ=2，
过B作BH垂直CQ,交CQ的延长线于H;则CH=CQ+QH,BH=HQ=
,
解得：BC2=BH2+CH2，BC=
故答案为.
练习册系列答案
相关题目
