��Ŀ����
����Ŀ����ͼ��ʾ����֪��ABC�У�AB=AC=BC=10���ף�M��N�ֱ�ӵ�A����Bͬʱ�������������εı��˶�����֪��M���ٶ���1����/����ٶȣ���N���ٶ���2����/�룬����N��һ�ε���B��ʱ��M��Nͬʱֹͣ�˶���
��1��M��Nͬʱ�˶������M��N�����غϣ�
��2��M��Nͬʱ�˶�����ɵõȱ���������AMN��
��3��M��N��BC�����˶�ʱ���ܷ�õ���MNΪ�ױߵĵ�����AMN��������ڣ��������ʱM��N�˶���ʱ�䣿

���𰸡�(1)10��;(2)![]() ��;(3)
��;(3)![]() ��.
��.
��������
��1���������M��N�˶�x���M��N�����غϣ���ʾ��M��N���˶�·�̣�N���˶�·�̱�M���˶�·�̶�10cm���г�������⼴�ɣ�
��2�������������M��N�˶�t��ɵõ��ȱ������Ρ�AMN��Ȼ���ʾ��AM��AN�ij������ڡ�A����60��������ֻҪAM=AN������ANM���ǵȱ������Σ�
��3�����ȼ����AMN�ǵ��������Σ���֤����ACM�ա�ABN���ɵ�CM=BN������˶�ʱ�䣬��ʾ��CM��NB�ij����г����̣��ɽ��δ֪����
��1�����M��N�˶�x���M��N�����غϣ�
x+10=2x�����x=10��
��2�����M��N�˶�t��ɵõ��ȱ���������AMN����ͼ����
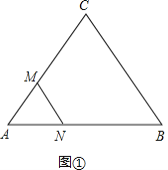
AM=t��AN=AB�CBN=10�C2t��
����������AMN�ǵȱ������Σ�
��t=10�C2t�����t=![]() ��
��
����M��N�˶�![]() ��ɵõ��ȱ���������AMN��
��ɵõ��ȱ���������AMN��
��3������M��N��BC�����˶�ʱ�����Եõ���MNΪ�ױߵĵ��������Σ�
�ɣ�1��֪10��ʱM��N�����غϣ�ǡ���ڵ�C����
��ͼ����������AMN�ǵ��������Σ�
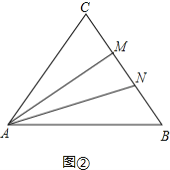
��AN=AM�����AMN=��ANM�����AMC=��ANB��
��AB=BC=AC�����ACB�ǵȱ������Σ����C=��B��
����ACM����ABN��
�� ��
��
���ACM�ա�ABN��AAS����
��CM=BN��
�赱��M��N��BC�����˶�ʱ��M��N�˶���ʱ��Ϊy��ʱ����AMN�ǵ��������Σ�
��CM=y�C10��NB=30�C2y��CM=NB��
y�C10=30�C2y��
��ã�y=![]() ���ʼ��������
���ʼ��������
������M��N��BC�����˶�ʱ���ܵõ���MNΪ�ױߵĵ�����AMN����ʱM��N�˶���ʱ��Ϊ![]() �룮
�룮

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д� ����������������ϵ�д�
����������������ϵ�д�