题目内容
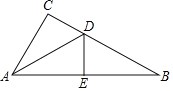
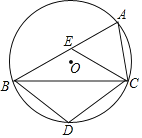
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
【答案】(1)证明见解析;(2)证明见解析;(3)①BC=4![]() ;②
;②![]()
【解析】(1)由菱形知∠D=∠BEC,由∠A+∠D=∠BEC+∠AEC=180°可得∠A=∠AEC,据此得证;
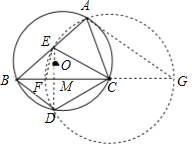
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG=AC=CE=CD,证△BEF∽△BGA得![]() ,即BFBG=BEAB,将BF=BC-CF=BC-AC、BG=BC+CG=BC+AC代入可得;
,即BFBG=BEAB,将BF=BC-CF=BC-AC、BG=BC+CG=BC+AC代入可得;
(3)①设AB=5k、AC=3k,由BC2-AC2=ABAC知BC=2![]() k,连接ED交BC于点M,Rt△DMC中由DC=AC=3k、MC=
k,连接ED交BC于点M,Rt△DMC中由DC=AC=3k、MC=![]() BC=
BC=![]() k求得DM=
k求得DM=![]() =
=![]() k,可知OM=OD-DM=3-
k,可知OM=OD-DM=3-![]() k,在Rt△COM中,由OM2+MC2=OC2可得答案.②设OM=d,则MD=3-d,MC2=OC2-OM2=9-d2,继而知BC2=(2MC)2=36-4d2、AC2=DC2=DM2+CM2=(3-d)2+9-d2,由(2)得ABAC=BC2-AC2,据此得出关于d的二次函数,利用二次函数的性质可得答案.
k,在Rt△COM中,由OM2+MC2=OC2可得答案.②设OM=d,则MD=3-d,MC2=OC2-OM2=9-d2,继而知BC2=(2MC)2=36-4d2、AC2=DC2=DM2+CM2=(3-d)2+9-d2,由(2)得ABAC=BC2-AC2,据此得出关于d的二次函数,利用二次函数的性质可得答案.
(1)∵四边形EBDC为菱形,
∴∠D=∠BEC,
∵四边形ABDC是圆的内接四边形,
∴∠A+∠D=180°,
又∠BEC+∠AEC=180°,
∴∠A=∠AEC,
∴AC=CE;
(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,
由(1)知AC=CE=CD,
∴CF=CG=AC,
∵四边形AEFG是⊙C的内接四边形,
∴∠G+∠AEF=180°,
又∵∠AEF+∠BEF=180°,
∴∠G=∠BEF,
∵∠EBF=∠GBA,
∴△BEF∽△BGA,
∴![]() ,即BFBG=BEAB,
,即BFBG=BEAB,
∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,
∴(BC﹣AC)(BC+AC)=ABAC,即BC2﹣AC2=ABAC;
(3)设AB=5k、AC=3k,
∵BC2﹣AC2=ABAC,
∴BC=2![]() k,
k,
连接ED交BC于点M,
∵四边形BDCE是菱形,
∴DE垂直平分BC,
则点E、O、M、D共线,
在Rt△DMC中,DC=AC=3k,MC=![]() BC=
BC=![]() k,
k,
∴DM=![]() ,
,
∴OM=OD﹣DM=3﹣![]() k,
k,
在Rt△COM中,由OM2+MC2=OC2得(3﹣![]() k)2+(
k)2+(![]() k)2=32,
k)2=32,
解得:k=![]() 或k=0(舍),
或k=0(舍),
∴BC=2![]() k=4
k=4![]() ;
;
②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,
∴BC2=(2MC)2=36﹣4d2,
AC2=DC2=DM2+CM2=(3﹣d)2+9﹣d2,
由(2)得ABAC=BC2﹣AC2
=﹣4d2+6d+18
=﹣4(d﹣![]() )2+
)2+![]() ,
,
∴当d=![]() ,即OM=
,即OM=![]() 时,ABAC最大,最大值为
时,ABAC最大,最大值为![]() ,
,
∴DC2=![]() ,
,
∴AC=DC=![]() ,
,
∴AB=![]() ,此时
,此时![]() .
.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
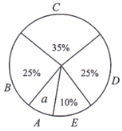
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.