题目内容
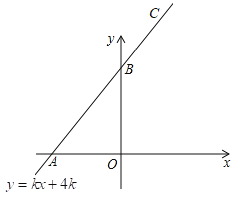
【题目】将一次函数
（
为常数）的图像位于
轴下方的部分沿轴翻折到轴上方，和一次函数（为常数）的图像位于轴及上方的部分组成“
”型折线，过点
作轴的平行线
，若该“”型折线在直线下方的点的横坐标满足
，则的取值范围是（ ）
A.
B.
C.
D.
【答案】A
【解析】
先解不等式3x+b＜1时，得x＜
；再求出函数y=3x+b沿x轴翻折后的解析式为y=-3x-b，解不等式-3x-b＜1，得x＞-
；根据x满足0＜x＜3，得出-=0，=3，进而求出b的取值范围．
∵y=3x+b，
∴当y＜1时，3x+b＜1，解得x＜；
∵函数y=3x+b沿x轴翻折后的解析式为-y=3x+b，即y=-3x-b，
∴当y＜1时，-3x-b＜1，解得x＞-；
∴-＜x＜，
∵x满足0＜x＜3，
∴-=0，=3，
∴b=-1，b=-8，
∴b的取值范围为-8≤b≤-1．
故选：A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
