题目内容
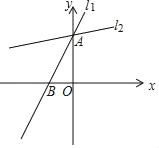
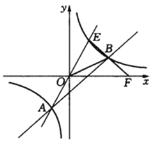
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A、E,AB交双曲线于另一点B(
交于点A、E,AB交双曲线于另一点B(![]() ,
,![]() ),连接EB并延长交x轴于点F.
),连接EB并延长交x轴于点F.
(1)![]() ;
;
(2)求直线AB的解析式;
(3)求△EOF的面积;
(4)若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.
【答案】(1)2;(2)y=x-2;(3)12;(4)(-4,-2)或(0,-6)或(8,10)
【解析】
(1)把B(![]() ,
,![]() )代入反比例函数
)代入反比例函数![]() 即可求出m的值;
即可求出m的值;
(2)联立直线y=2x与反比例函数![]() 即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
(3)先用待定系数法求出EB的解析式,再令y=0,得出F的坐标,最后用三角形的面积公式求出△EOF的面积;
(4)分类讨论:分别以AB,BE,AE为对角线求对应的P的坐标.
(1)∵点B(2m,m)在反比例函数![]() 上,
上,
∴2m·m=8,解得m=±2,而m>0,
∴m=2
(2)m=2,则点B的坐标为(4,2)
联立解析式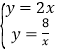 得
得![]() 或
或![]()
∴点A坐标为(-2,-4),E点坐标为(2,4)
设直线AB的解析式为y=k1x+b1,
把A(-2,-4),B(4,2)代入得:-2k1+b1=-4,4k1+b1=2,
解方程组得k1=1, b1=-2,
∴直线AB的解析式为y=x-2;
(3)设直线EB的解析式为y=k2x+b2,
把E(2,4),B(4,2)代入可得2k2+b2=4,4k2+b2=2,解得k2=-1,b2=6,
∴直线EB的解析式为y=-x+6,
令y=0,解得x=6,故F(6,0)
∴S△EOF=![]() =12
=12
(4)①以AB为对角线时,由A(-2,-4),B(4,2)求出中点O坐标为(1,-1),故E(2,4)关于中点O(1,-1)的对称点P为(0,-6);
②以BE为对角线时,由E(2,4),B(4,2)求出中点O’坐标为(3,3),故A(-2,-4)关于中点O’(3,3)的对称点P为(8,10);
③以AE为对角线时,由A(-2,-4),E(2,4)求出中点O’坐标为(0,0),故B(4,2)关于中点O’(0,0)的对称点P为(-4,-2);
故满足条件的点P的坐标为(-4,-2)或(0,-6)或(8,10)

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案