Question

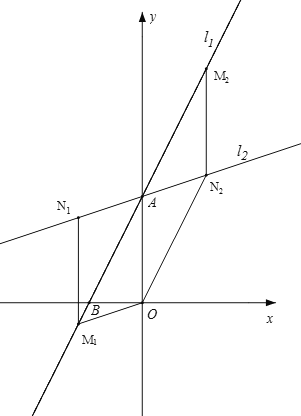
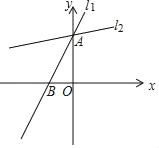
【题目】如图，已知直线l1：y＝2x+4与y轴交于A点，与x轴交于点B，经过A点的直线l2与直线l1所夹的锐角为45°．

（1）过点B作CB⊥AB，交l2于C，求点C的坐标．

（2）求l2的函数解析式．

（3）在直线l1上存在点M，直线l2上存在点N，使得点A、O、M、N四点组成的四边形是平行四边形，请直接写出点N的坐标．

Answer 1

【答案】（1）C(-6，2)；（2）；（3） 或

【解析】

(1)过作CD⊥x轴于点D，易证△BDC≌△AOB，由此可得BD=OA，CD=OB，由直线：，可得A（0，4），B（-2，0），可得BD=OA=4，CD=OB=2，有OD=4+2=6 ，即可求得点C坐标；

(2)利用待定系数法进行求解即可；

（3）分OA为平行四边形的边和OA为平行四边形的对角线，画出图形，结合平行四边形的性质进行求解即可.

(1)过作CD⊥x轴于点D，

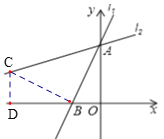
∵CB⊥AB，

∴∠ABC=90°，∴∠CBD+∠ABO=90°，

又∵∠BAC=45°，

∴∠ACB=90°-∠BAC=45°=∠BAC，

∴BC=BA，

∵∠AOB=90°，∴∠ABO+∠BAO=90°，

∴∠CBD=∠BAO，

又∵∠BDC=∠AOB=90°，

∴△BDC≌△AOB，

∴BD=OA，CD=OB，

∵直线：，

∴A（0，4），B（-2，0），

∴BD=OA=4，CD=OB=2，

∴OD=4+2=6 ，

∴C(-6，2)；

(2)设的解析式为

∵A（0，4），C(-6，2)，

∴，

∴

∴；

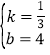
（3）如图，OA为平行四边形的边时，

当四边形AOM1N1为平行四边形时，有M1N1=AO=4，

即（）-（）=4，解得：x=，

当x=时，=，

所以N1（）；

当四边形AOM2N2为平行四边形时，有M2N2=AO=4，

即（）-（）=4，解得：x=，

当x=时，=，

所以N2（）；

OA为平行四边形的对角线时，由上可知AM1ON2为平行四边形，此时N2（）；

综上可知N点坐标为 或，

故答案为： 或.