Question

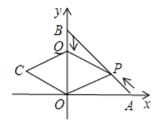
【题目】如图，A，B两点的坐标分别为（6,0),(0,6)，点P从点A出发，沿AB方向以每秒个单位的速度向终点B运动；同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动，将△PQO沿BO翻折，点P的对应点为点C，若四边形QPOC为菱形，则点C的坐标为________．

Answer 1

【答案】(-4,2)

【解析】

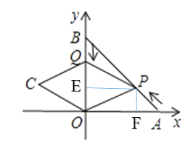
过P点作PE⊥y轴于E点，作PF⊥x轴于F点，根据翻折的性质，要使四边形QPOC为菱形，由于PC⊥OQ,只需QE=OE即可，设运动了t秒，则BQ=t，OQ=6-t,AP=t，由等腰直角△APF得PF=t，故在矩形EPFO中，PF=EO=t，令OQ=2 EO，即可求出t，再求出Q点坐标即可.

过P点作PE⊥y轴于E点，作PF⊥x轴于F点，

设运动了t秒，则BQ=t，OQ=6-t,AP=t，由等腰直角△APF得PF=t，

要使四边形QPOC为菱形，由于PC⊥OQ,只需QE=OE即可，

在矩形EPFO中，PF=EO=t

OQ=2 EO，

即6-t=2t,解得t=2，故Q（0,4），E（0,2）P（4,2）

故C（-4,2）