题目内容
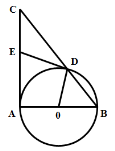
【题目】如图,□ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.

(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
【答案】(1)证明见解析(2)证明见解析
【解析】
试题分析:(1)根据平行四边形的性质和条件得出OB=OE=OD,然后可得∠CEO=∠CDE,∠DBE=∠CDE,根据三角形的内角和得出∠BED=90°即可得出结论;(2)根据条件证明△BDE∽△CDE,然后利用相似三角形的性质可得出结论.
试题解析:(1)∵四边形ABCD是平行四边形,∴BO=![]() BD,∵OE=OB,∴OE=
BD,∵OE=OB,∴OE=![]() BD,∴OB=OE=OD,∴∠CEO=∠CDE,∠DBE=∠CDE,又∠CEO+∠CDE+∠DBE+∠CDE=180°,∴∠BED=90°,∴DE⊥BE;
BD,∴OB=OE=OD,∴∠CEO=∠CDE,∠DBE=∠CDE,又∠CEO+∠CDE+∠DBE+∠CDE=180°,∴∠BED=90°,∴DE⊥BE;
(2)∵OE⊥CD ,∴∠CEO+∠DCE=∠CDE+∠CE=D,∴△BDE∽△CDE,∴BD:CD=DE:CE,
∴BDCE=CDDE.

练习册系列答案
相关题目