题目内容
【题目】若一个正整数，它的各位数字是左右对称的，则称这个数是对称数．如
，
，
都是对称数，最小的对称数是
，但没有最大的对称数，因为数位是无穷的．
若将任意一个四位对称数分解为前两位数表示的数和后两位数表示的数，请你证明：这两个数的差一定能被
整除；
设一个三位对称数为
（
），该对称数与相乘后得到一个四位数，该四位数前两位所表示的数和后两位所表示的数相等，且该四位数各位数字之和为8，求这个三位对称数．
【答案】（1）证明见解析（2）202
【解析】
设四位对称数分解为前两位数所表示的数为：
，和后两位数所表示的数为
，用
的代数式表示这两个数的差即可解决问题．
设这个三位对称数为：
乘以11的结果千位，百位，十位，个位上的数分别为a,a+b,a+b,a，根据题意列方程组即可．
(1)设四位对称数分解为前两位数所表示的数为：，
和后两位数所表示的数为，
由题意(
为整数,
是整数，
一定能被9整除，
∴这两个数的差一定能被9整除.
(2)设这个三位对称数为：
乘以11的结果千位，百位，十位，个位上的数分别为a,a+b,a+b,a
由题意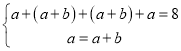
=2
∴满足条件的三位对称数为202.
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
