题目内容
【题目】已知:如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() 分别平分正方形的两个外角,且满足
分别平分正方形的两个外角,且满足![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数.
的度数.
【答案】(1)详见解析;(2)135°.
【解析】
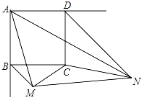
(1)如图(3)由条件可以得出∠BMA=∠3,∠ABM=∠ADN=135°,就可以得出△ABM∽△NDA,利用相似三角形的性质就可以得出BMDN=36;
(2)由△ABM∽△NDA,可以得出BM:DA=AB:ND,再由正方形的性质通过等量代换就可以得出△BCM∽△DNC.利用角的关系和圆周角的度数就可以求出结论;
(3)将△AND绕点A顺时针旋转90°得到△ABF,连接MF,证明△ABF≌△ADN.利用边角的关系得出△BMF是直角三角形,由勾股定理就可以得出结论.
![]() 证明:
证明:
∵![]() ,
,![]() 分别平分正方形的两个外角,
分别平分正方形的两个外角,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
![]() ∵
∵![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目