题目内容
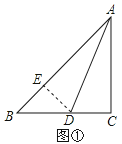
【题目】已知,如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
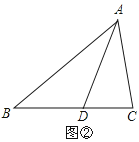
(1)作出边AC的垂直平分线DE;
(2)当AE=BC时,求∠A的度数.
【答案】(1)画图见解析(2)∠A=20°
【解析】试题分析:(1)分别以点A、C为圆心,以大于![]() AC长度为半径画弧,两弧在AC两边相交于,然后过这两点作直线DE即可;
AC长度为半径画弧,两弧在AC两边相交于,然后过这两点作直线DE即可;
(2)连接CE,根据线段垂直平分线上的点到线段两端点的距离相等可得AE=CE,设∠A=x,然后根据等边对等角的性质以及等腰三角形两底角相等表示出∠ACB,然后列出方程求解即可.
试题解析:(1)如图,分别以点A、C为圆心,大于![]() AC长为半径画弧,两条弧相交于两点,作过这两点的直线,与AC、AB分别相交于点D、E,则直线DE即为所求;
AC长为半径画弧,两条弧相交于两点,作过这两点的直线,与AC、AB分别相交于点D、E,则直线DE即为所求;
(2)如图,连接CE,
∵DE是AC的垂直平分线,∴AE=CE,∴∠A=∠ACE,
∵AE=BC,∴CE=BC,∴∠B=∠CEB,
设∠A=x,
则∠CEB=∠A+∠ACE=x+x=2x,
在△BCE中,∠BCE=180°-2×2x=180°-4x,
∴∠ACB=∠ACE+∠BCE=x+180°-4x=120°,
解得x=20°,
即∠A=20°.


练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目