题目内容
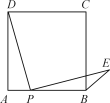
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )
A. 75° B. 60° C. 45° D. 30°
【答案】C
【解析】
过E作AB的延长线AF的垂线,垂足为F,可得出∠F为直角,先利用AAS证明△ADP≌△PEF,根据全等三角形的对应边相等可得出AD=PF,AP=EF,再由正方形的边长相等得到AD=AB,由AP+PB=PB+BF,得到AP=BF,等量代换可得出EF=BF,即三角形BEF为等腰直角三角形,可得出∠EBF为45°,再由∠CBF为直角,即可求出∠CBE的度数.
过点E作EF⊥AF,交AB的延长线于点F,则∠F=90°,
∵四边形ABCD为正方形,
∴AD=AB,∠A=∠ABC=90°,
∴∠ADP+∠APD=90°,
由旋转可得:PD=PE,∠DPE=90°,
∴∠APD+∠EPF=90°,
∴∠ADP=∠EPF,
在△APD和△FEP中
∠ADP=∠FPE
∠A=∠F=90°
PD=EP,
∴△APD≌△FEP(AAS),
∴AP=EF,AD=PF,
又∵AD=AB,
∴PF=AB,即AP+PB=PB+BF,
∴AP=BF,
∴BF=EF,又∠F=91°,
∴△BEF为等腰直角三角形,
∴∠EBF=45°,又∠CBF=91°,
则∠CBE=45°.
故选C.

练习册系列答案
相关题目