题目内容
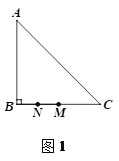
【题目】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM(点D与点A对应,点E与点B对应),DM交AC于点P.
(1)若点N是线段MB的中点,如图1.
① 依题意补全图1;
② 求DP的长;
(2)若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)①根据题意补充图形即可;
②连接AD.在Rt△ABN中,由勾股定理得AN的长.由平移的性质得到DM=AN,
进而得到△ADP∽△CMP,由相似三角形的性质即可得到结论.
(2)连接![]() ,先证四边形
,先证四边形![]() 是平行四边形.由平行四边形的性质得到
是平行四边形.由平行四边形的性质得到![]() ∥
∥![]() ,再由平行线的性质得到
,再由平行线的性质得到![]() .进而得到
.进而得到![]() .由平行线分线段成比例定理得到
.由平行线分线段成比例定理得到![]() .由此得到NB的长,即可得到结论.
.由此得到NB的长,即可得到结论.
详解:(1)①如图1,补全图形.
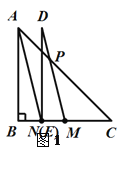
② 连接AD,如图2.
在Rt△ABN中,∵∠B=90°,AB=4,BN=1,∴![]() .
.
∵线段AN平移得到线段DM,∴DM=AN=![]() ,AD=NM=1,AD∥MC,
,AD=NM=1,AD∥MC,
∴△ADP∽△CMP.
∴![]() .
.
∴![]() .
.

(2)连接![]() ,如图3.
,如图3.
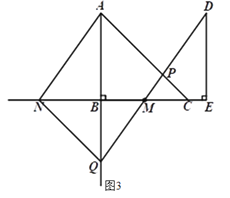
由平移知:![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ∥
∥![]() ,且
,且![]() =
=![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ∥
∥![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ∥
∥![]() ,
,
∴![]() .
.
又∵![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
∴![]() .
.
∴![]() (舍去负数).
(舍去负数).
∴![]() .
.
∴![]() .
.
方法二,连接AD,如图4.

设CE长为x.
∵线段AB移动到得到线段DE,
∴![]() ,AD∥BM.
,AD∥BM.
∴△ADP∽△CMP.
∴![]() .
.
∵MQ=DP,
∴![]() .
.
∵△QBM∽△QAD,
∴![]() .
.
解得:![]() .
.
∴![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目