题目内容
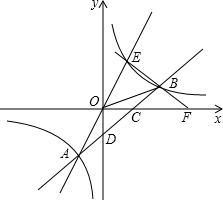
如图,直线y=3x+3与x轴交于A点,与y轴交于B点,以AB为直角边作等腰Rt△ABC,∠BAC=90°,AC=AB,双曲线y=
经过C点
①求双曲线的解析式;
②点P为第四象限双曲线上一点,连接BP,点Q(x、y)为线段AB上一动点,过Q作QD⊥BP,若QD=n,问是否存在一点P使y+n=3?若存在,求直线BP解析式;若不存在,说明理由.
| k |
| x |
①求双曲线的解析式;
②点P为第四象限双曲线上一点,连接BP,点Q(x、y)为线段AB上一动点,过Q作QD⊥BP,若QD=n,问是否存在一点P使y+n=3?若存在,求直线BP解析式;若不存在,说明理由.

①过点C作CD⊥x轴于点D.
由y=3x+3得,A(-1,0),B(0,3),
∴OA=1,OB=3.
∵∠CAD+∠BAO=90°,∠ABO+∠BAO=90°,
∴∠CAD=∠AOB.
∵AC=AB,∠CAD=∠AOB=90°,
∴△ADC≌△BOA,
∴CD=OA=1,AD=OB=3,
∴OD=OA+AD=4,
∴C(-4,1),
∴k=xy=(-4)×1=-4,
∴该双曲线的解析式是y=-
;
②过点Q作QM⊥x轴于点M,QN⊥y轴于点N.
∵∠MON=90°,
∴四边形OMQN是矩形,
∴QM=ON.
∵y+n=3,OM=3,
∴ON+QD=OB,
∵ON+BN=OB,
∴QD=BN.
∵∠QNB=∠BDQ=90°,BQ=QB,
∴△BQN≌△QBD,
∴∠BQN=∠QBD,
∵QN∥OA,
∴∠BQN=∠BAO,
∴∠BAO=∠QBD,
∴AE=DE.
设OE=x.则BE=AE=x+1.
在直角△BOE中,由勾股定理,得
32+x2=(x+1)2,
解得,x=4,
∴E(4,0).
设直线BP的解析式是:y=kx+b(k≠0)
∴
,
解得
,
∴y=-
x+3.

由y=3x+3得,A(-1,0),B(0,3),
∴OA=1,OB=3.
∵∠CAD+∠BAO=90°,∠ABO+∠BAO=90°,
∴∠CAD=∠AOB.
∵AC=AB,∠CAD=∠AOB=90°,
∴△ADC≌△BOA,
∴CD=OA=1,AD=OB=3,
∴OD=OA+AD=4,
∴C(-4,1),
∴k=xy=(-4)×1=-4,
∴该双曲线的解析式是y=-
| 4 |
| x |
②过点Q作QM⊥x轴于点M,QN⊥y轴于点N.
∵∠MON=90°,
∴四边形OMQN是矩形,
∴QM=ON.
∵y+n=3,OM=3,
∴ON+QD=OB,
∵ON+BN=OB,
∴QD=BN.
∵∠QNB=∠BDQ=90°,BQ=QB,
∴△BQN≌△QBD,
∴∠BQN=∠QBD,
∵QN∥OA,
∴∠BQN=∠BAO,
∴∠BAO=∠QBD,
∴AE=DE.
设OE=x.则BE=AE=x+1.
在直角△BOE中,由勾股定理,得
32+x2=(x+1)2,
解得,x=4,
∴E(4,0).
设直线BP的解析式是:y=kx+b(k≠0)
∴
|
解得
|
∴y=-
| 3 |
| 4 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 ,一次函数图象与y轴的交点为C.
,一次函数图象与y轴的交点为C.








