ЬтФПФкШн
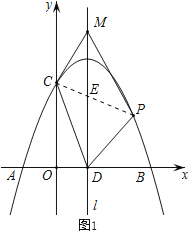
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпyЃНЉx2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкCЕуЃЌЕуPЪЧХзЮяЯпЩЯдкЕквЛЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕуPЕФКсзјБъЮЊtЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЩшХзЮяЯпЕФЖдГЦжсЮЊlЃЌlгыxжсЕФНЛЕуЮЊDЃЎдкжБЯпlЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгBCЃЌPBЃЌPCЃЌЩшЁїPBCЕФУцЛ§ЮЊSЃЎЧѓSЙигкtЕФКЏЪ§БэДяЪНЃЛВЂЧѓSзюДѓЪБЕуPЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЛЃЈ2ЃЉдкжБЯпlЩЯДцдкЕуMЃЌЪЙЕУЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃЌЕуMЕФзјБъЮЊЃЈ1ЃЌ6ЃЉЃЛЃЈ3ЃЉSЃНЉ![]() t2+
t2+![]() tЃЌЕБt ЃН
tЃЌЕБt ЃН![]() ЪБЃЌSгазюДѓжЕЃЌДЫЪБPЃЈ
ЪБЃЌSгазюДѓжЕЃЌДЫЪБPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉАбЕуAЁЂBзјБъДњШыyЃНЉx2+bx+cЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЯШЧѓГіCЁЂDзјБъЃЌМйЩшжБЯпlЩЯДцдкЕуMЃЌЪЙЕУЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃЌИљОнЦНааЫФБпаЮаджЪЃЌЧѓГіЕуPзјБъЃЌНјЖјЧѓГіЕуMзјБъЃЛ
ЃЈ3ЃЉЙ§ЕуPзїPFЁЮyжсЃЌНЛBCгкЕуFЃЌЧѓГіжБЯпBCНтЮіЪНЃЌБэЪОГіЯпЖЮPFГЄЃЌИљОн![]() МДПЩЕУЕНSЙигкtЕФКЏЪ§НтЮіЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЎ
МДПЩЕУЕНSЙигкtЕФКЏЪ§НтЮіЪНЃЌдйИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉНЋAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉДњШыyЃНЉx2+bx+cЃЌ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФБэДяЪНЮЊyЃНЉx2+2x+3ЃЎ
ЃЈ2ЃЉдкЭМ1жаЃЌСЌНгPCЃЌНЛХзЮяЯпЖдГЦжсlгкЕуEЃЌ
ЁпХзЮяЯпyЃНЉx2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌ
ЁрХзЮяЯпЕФЖдГЦжсЮЊжБЯпxЃН1ЃЎ
ЕБxЃН0ЪБЃЌyЃНЉx2+2x+3ЃН3ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЎ
ШєЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃЌдђCEЃНPEЃЌDEЃНMEЃЌ
ЁпЕуCЕФКсзјБъЮЊ0ЃЌЕуEЕФКсзјБъЮЊ1ЃЌ
ЁрЕуPЕФКсзјБъtЃН1ЁС2Љ0ЃН2ЃЌ
ЁрЕуPЕФзјБъЮЊЃЈ2ЃЌ3ЃЉЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ1ЃЌ3ЃЉЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ1ЃЌ6ЃЉЃЎ
ЙЪдкжБЯпlЩЯДцдкЕуMЃЌЪЙЕУЫФБпаЮCDPMЪЧЦНааЫФБпаЮЃЌЕуMЕФзјБъЮЊЃЈ1ЃЌ6ЃЉЃЎ
ЃЈ3ЃЉдкЭМ2жаЃЌЙ§ЕуPзїPFЁЮyжсЃЌНЛBCгкЕуFЃЎ
ЩшжБЯпBCЕФНтЮіЪНЮЊyЃНmx+nЃЈmЁй0ЃЉЃЌ
НЋBЃЈ3ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉДњШыyЃНmx+nЃЌ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊyЃНЉx+3ЃЎ
ЁпЕуPЕФзјБъЮЊЃЈtЃЌЉt2+2t+3ЃЉЃЌ
ЁрЕуFЕФзјБъЮЊЃЈtЃЌЉt+3ЃЉЃЌ
ЁрPFЃНЉt2+2t+3ЉЃЈЉt+3ЃЉЃНЉt2+3tЃЌ
Ёр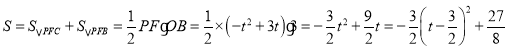 ЃЌ
ЃЌ
ЁрЕБt ЃН![]() ЪБЃЌSгазюДѓжЕЃЌДЫЪБPЃЈ
ЪБЃЌSгазюДѓжЕЃЌДЫЪБPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
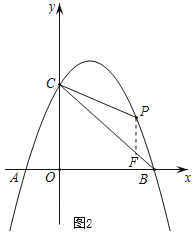

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ