题目内容
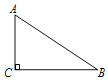
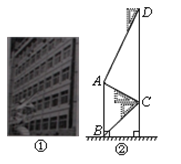
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图11①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图10②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73)
=1.73)
【答案】雕塑AB的高度约为6.8米
【解析】
过点C作CE⊥AB于E,根据题目已知条件可以求出AC=5,利用解直角三角形可以求出AE和CE的长度,从而进一步求出BE,即可求得AB=AE+BE.
解:如图,过点C作CE⊥AB于E.
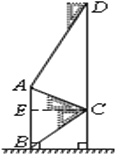
∵∠D=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=10,∴AC=![]() CD=5.
CD=5.
在Rt△ACE中,
AE=ACsin∠ACE=5sin30°=![]() ,
,
CE=ACcos∠ACE=5cos30°=![]() .
.
在Rt△BCE中,
∵∠BCE=45°,
∴BE=CEtan45°=![]() ,
,
∴AB=AE+BE=![]() +
+![]() =
=![]() (
(![]() +1)≈6.8(米).所以,雕塑AB的高度约为6.8米.
+1)≈6.8(米).所以,雕塑AB的高度约为6.8米.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
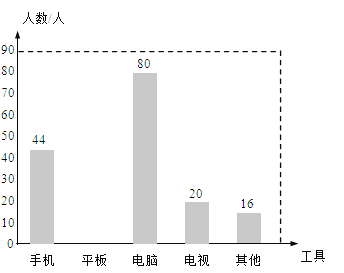
【题目】在“停课不停学”期间,某校数学兴趣小组对本校同学观看教学视频所使用的工具进行了调查,并从中随机抽取部分数据进行分析,将分析结果绘制成了两幅不完整的统计表与统计图.
工具 | 人数 | 频率 |
手机 | 44 | a |
平板 | b | 0.2 |
电脑 | 80 | c |
电视 | 20 | d |
不确定 | 16 | 0.08 |
请根据上述信息回答下列问题:
(1)所抽取出来的同学共 人,表中a= ,b= ;
(2)请补全条形统计图;
(3)若该校观看教学视频的学生总人数为2500人,则使用电脑的学生人数约 人.![]()