题目内容
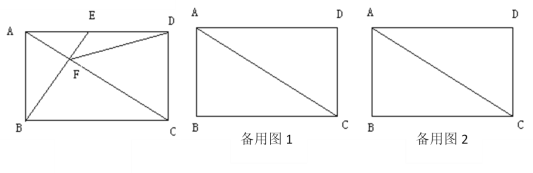
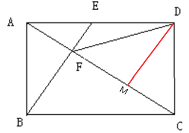
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E在AD上,BE与AC交于点F.
(1)若AC⊥BE,求AE的长 ;
(2)设△DEF和△DCF的面积分别为S1和S2,当AE=m时,求S1:S2;
(3)当AE的长是多少时,△DCF是等腰三角形?
【答案】(1)![]() ;(2)S1:S2=m(4-m):16;(3)
;(2)S1:S2=m(4-m):16;(3)![]() 、4、
、4、![]() .
.
【解析】
(1)利用已知条件,得到,![]() ,得到
,得到![]() ,代入求值可得到AE.
,代入求值可得到AE.
(2)过F作BC,AD的垂线,长度分别为h1和h2,根据△AEF∽△CBF和△AGF∽△CBA,得到![]() 可以求得
可以求得![]() 代入可得到比值.
代入可得到比值.
(3)分三种情况进行讨论,分别是CD=CF=3,DF=CF,DF=CD=3分开讨论即可得到结果.
(1)∵四边形ABCD是矩形;
∴△ABE是直角三角形;
又∵AC⊥BE,
∴∠AFB=90°,
∴∠ABE+∠AEB=∠ABE+∠BAC=90°.
∴∠AEB=∠BAC
∴![]() ,
,
∴![]() ;
;
∴![]()
(2)
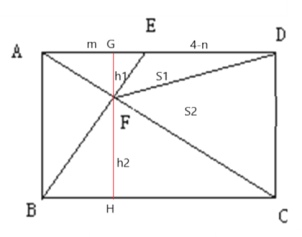
过F作BC,AD的垂线,长度分别为h1和h2,
∵△AEF∽△CBF,
∴![]() ,
,
∵h1+h2=3,
∴![]()
又∵△AGF∽△CBA,
∴![]()
∴![]()
∴![]()
∴S1:S2=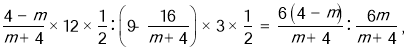
∴S1:S2=m(4-m):16
(3)本题分三种情况:①当CD=CF=3时,AF=2,由(1)得AE:BC=AF:FC,∴AE=![]() ;
;
②当DF=CF时,F为AC的中点,此时E、D重合,∴AE=4;
③当DF=CD=3时,作DM⊥AC于G,则CM=FM=![]() ,AF=
,AF=![]() ,
,
由(1)得AE:BC=AF:FC,∴AE=![]()
综上,AE=![]() 、4、
、4、![]()

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?