题目内容
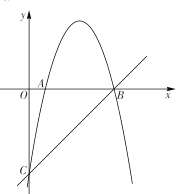
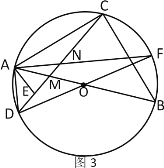
【题目】如图,反比例函数y=![]() (x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
(x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
【答案】9
【解析】
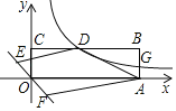
延长DE交x轴于K,作DH⊥OA于H,证得△OEK≌△OFA,即可证得S四边形ADEF=S四边形ADEO+S△KEO=S△ADK,设G(a,![]() ),用a表示OA和AB,根据三角形面积公式求得即可结果.
),用a表示OA和AB,根据三角形面积公式求得即可结果.
解:延长DE交x轴于K,作DH⊥OA于

设G(a,![]() ),则OA=a,AG=
),则OA=a,AG=![]() ,
,
∵BG=2GA,
∴![]() ,
,
∴DH=AB=AG+BG=![]() ,
,
∵DE∥AF,
∴∠EKO=∠FAO,
在△OEK和△OFA中,
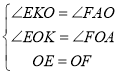 ,
,
∴△OEK≌△OFA(AAS),
∴OK=OA=a,
∴AK=2a,
∴S四边形ADEF=S四边形ADEO+S△KEO=S△ADK
=![]() ;
;
故答案为:9.

练习册系列答案
相关题目