题目内容
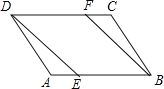
【题目】如图,在平行四边形ABCD中,∠ABC=45°,AB=4![]() ,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.
,BC=9,直线MN平分平行四边形ABCD的面积,分别交边AD、BC于点M、N,若△BMN是以MN为腰的等腰三角形,则BN=_____.

【答案】![]() 或5
或5
【解析】
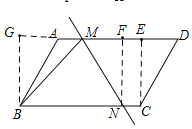
如图,过点C作CE⊥AD于E,过点N作NF⊥AD于F,过点B作BG⊥AD,与DA的延长线交于点G.然后分2种情况:①当MN=MB;②当MN=BN时进行分析即可.
解:如图,过点C作CE⊥AD于E,过点N作NF⊥AD于F,过点B作BG⊥AD,与DA的延长线交于点G.
∵直线MN平分平行四边形ABCD的面积,
∴AM=CN,
设AM=CN=x,则EF=x,BN=9﹣x
∵∠ABC=45°,AB=4![]() ,
,
∴GB=GA=4,DE=4,
∴MF=5﹣2x,
在Rt△BGM中,BM2=42+(4+x)2,
在Rt△NFM中,MN2=42+(5﹣2x)2,
∵△BMN是以MN为腰的等腰三角形,
∴①当MN=MB时,易证Rt△MFN≌Rt△MGB(HL),
MF=MG,
即5﹣2x=x+4,
解得x=![]() ,即CN=
,即CN=![]() ,
,
∴BN=BC﹣CN=9﹣![]() =
=![]()
②当MN=BN时,MN2=BN2,
∴42+(5﹣2x)2=(9﹣x)2,
解得x1=4,x2=﹣![]() (不符合题意,舍去),
(不符合题意,舍去),
MN2=42+(5﹣2x)2=16+(5﹣2×4)2=25,
∴MN=5,
∴BN=5
故答案为![]() 或5.
或5.

练习册系列答案
相关题目