Question

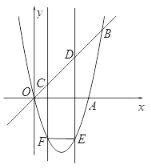
【题目】如图，在平面直角坐标系xOy中，函数的图象经过点，作AC⊥x轴于点C．

（1）求k的值；

（2）直线AB：图象经过点交x轴于点．横、纵坐标都是整数的点叫做整点．线段AB，AC，BC围成的区域（不含边界）为W．

①直线AB经过时，直接写出区域W内的整点个数；

②若区域W内恰有1个整点，结合函数图象，求a的取值范围．

Answer 1

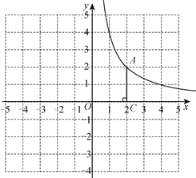
【答案】（1）k=4； （2）①1个； ②当时区域W内恰有1个整点．

【解析】

（1）把A（2，2）代入y=中便可求得k；

（2）①根据图象直接写出答案便可；

②用待定系数法求出直线AB分别过点（0，1），（1，0），（3，1），（4，1）四点时的a值便可．

解：（1）把A（2，2）代入y=中，得k=2×2=4；

（2）①∵直线AB经过（0，1），设直线AB的解析式为：y=ax+b（a≠0），则

，

解得，

∴直线AB的解析式为：y=x+1，

∴B（-2，0），

图象如下：

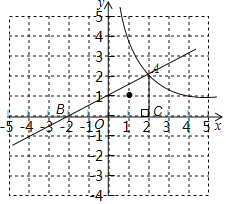
由图象可知，直线AB经过（0，1）时，区域W内的整点只有1个；

②当直线AB经过点A（2，2），（0，1）时区域W内恰有1个整点，则

，

∴a＝，

当直线AB经过点A（2，2），（1，1）时区域W内没有整点，则

，

∴a=1，

∴当≤a＜1时区域W内恰有1个整点；

综上，当≤a＜1时区W内恰有1个整点．