题目内容
【题目】如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
(1)求此抛物线所对应的函数表达式.
(2)求PF的长度,用含m的代数式表示.
(3)当四边形PEDF为平行四边形时,求m的值.
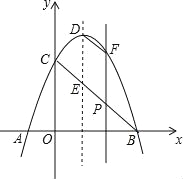
【答案】(1)y=-x2+2x+3;(2)-m2+3m.(3)2.
【解析】
试题分析:(1)根据待定系数法,可得函数解析式;
(2)根据自变量与函数值的对应关系,可得C点坐标,根据平行于y轴的直线上两点之间的距离是较大的纵坐标减较的纵坐标,可得答案;
(3)根据自变量与函数值的对应关系,可得F点坐标,根据平行于y轴的直线上两点之间的距离是较大的纵坐标减较的纵坐标,可得DE的长,根据平行四边形的对边相等,可得关于m的方程,根据解方程,可得m的值.
试题解析:(1)∵点A(-1,0),点B(3,0)在抛物线y=-x2+bx+c上,
∴![]() ,解得
,解得![]() ,
,
此抛物线所对应的函数表达式y=-x2+2x+3;
(2)∵此抛物线所对应的函数表达式y=-x2+2x+3,
∴C(0,3).
设BC所在的直线的函数解析式为y=kx+b,将B、C点的坐标代入函数解析式,得
![]() ,解得
,解得![]() ,
,
即BC的函数解析式为y=-x+3.
由P在BC上,F在抛物线上,得
P(m,-m+3),F(m,-m2+2m+3).
PF=-m2+2m+3-(-m+3)=-m2+3m.
(3)如图
 ,
,
∵此抛物线所对应的函数表达式y=-x2+2x+3,
∴D(1,4).
∵线段BC与抛物线的对称轴交于点E,
当x=1时,y=-x+3=2,
∴E(1,2),
∴DE=4-2=2.
由四边形PEDF为平行四边形,得
PF=DE,即-m2+3m=2,
解得m1=1,m2=2.
当m=1时,线段PF与DE重合,m=1(不符合题意,舍).
当m=2时,四边形PEDF为平行四边形.