题目内容
【题目】如图,以![]() 的直角边
的直角边![]() 为直径作
为直径作![]() 交斜边
交斜边![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证: ![]()
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的值.
的值.
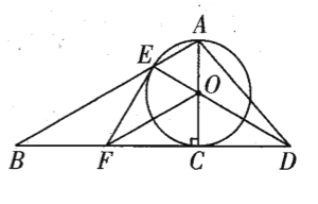
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接![]() ,由
,由![]() 是直径,可得
是直径,可得![]() ,结合
,结合![]() ,即可得到结论;
,即可得到结论;
(2)由垂径定理得:直线![]() 垂直平分
垂直平分![]() ,从而得
,从而得![]() ,结合
,结合![]() ,即可得到结论;
,即可得到结论;
(3)过点![]() 作
作![]() 于点
于点![]() ,易证
,易证![]() 是等边三角形,
是等边三角形,![]() ,AH=
,AH=![]() ,在RtOCD中,OD=6,从而得
,在RtOCD中,OD=6,从而得![]() ,根据正切三角函数的定义,即可求解.
,根据正切三角函数的定义,即可求解.
(1)连接![]() ,
,
![]() 是直径,
是直径,
∴∠AEC=90°,即:![]() ,
,
∵![]() ,
,
![]() ;
;
(2)![]() ,
,
∴直线![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即:OE⊥EF,
,即:OE⊥EF,
∴![]() 是
是![]() 的切线;
的切线;
(3)过点![]() 作
作![]() 于点
于点![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,AH=
,AH=![]() OH=
OH=![]() ,∠AOE=∠COD=60°,
,∠AOE=∠COD=60°,
∴在RtOCD中,OD=2OC=2×3=6,
∴![]() ,
,
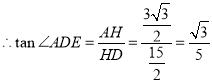 .
.


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】某企业对一种设备进行升级改造,并在一定时间内进行生产营销,设改造设备的台数为x,现有甲、乙两种改造方案.
甲方案:升级后每台设备的生产营销利润为4000元,但改造支出费用![]() 由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为
由材料费和施工费以及其他费用三部分组成,其中材料费与x的平方成正比,施工费与x成正比,其他费用为2500元,(利润=生产营销利润-改造支出费用).设甲方案的利润为![]() (元),经过统计,得到如下数据:
(元),经过统计,得到如下数据:
改造设备台数x(台) | 20 | 40 |
利润 | 9500 | 5500 |
乙方案:升级后每台设备的生产营销利润为3500元,但改造支出费用![]() 与x之间满足函数关系式:
与x之间满足函数关系式:![]() (a为常数,
(a为常数,![]() ),且在使用过程中一共还需支出维护费用
),且在使用过程中一共还需支出维护费用![]() ,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为
,(利润=生产营销利润-改造支出费用-维护费用).设乙方案的利润为![]() (元).
(元).
(1)分别求出![]() ,
,![]() 与x的函数关系式;
与x的函数关系式;
(2)若![]() ,
,![]() 的最大值相等,求a的值;
的最大值相等,求a的值;
(3)如果要将30台设备升级改造,请你帮助决策,该企业应选哪种方案,所获得的利润较大.