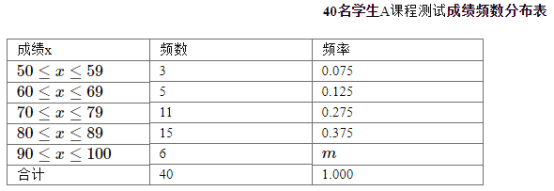
题目内容
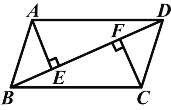
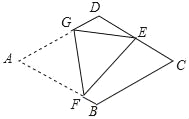
【题目】如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则tan∠EFG的值为_____.
【答案】![]()
【解析】分析:连接AE交GF于O,连接BE,BD,在Rt△BCE中,利用锐角三角函数求出CE的值,在Rt△ABE中,利用勾股定理求出AE的值.由折叠可知,AE⊥GF,EO=![]() AE. 设AF=x=EF,根据BF2+BE2=EF2,列方程求出x的值,进而求出tan∠EFG的值.
AE. 设AF=x=EF,根据BF2+BE2=EF2,列方程求出x的值,进而求出tan∠EFG的值.
详情:如图,连接AE交GF于O,连接BE,BD,则△BCD为等边三角形,
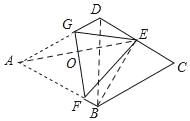
∵E是CD的中点,
∴BE⊥CD,
∴∠EBF=∠BEC=90°,
Rt△BCE中,CE=cos60°×3=1.5,BE=sin60°×3=![]() ,
,
∴Rt△ABE中,AE=![]() =
=![]() ,
,
由折叠可得,AE⊥GF,EO=![]() AE=
AE=![]() ,
,
设AF=x=EF,则BF=3﹣x,
∵Rt△BEF中,BF2+BE2=EF2,
∴(3﹣x)2+(![]() )2=x2,
)2=x2,
解得x=![]() ,即EF=
,即EF=![]() ,
,
∴Rt△EOF中,OF=![]() ,
,
∴tan∠EFG=![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目