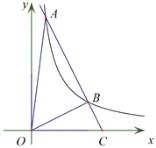
题目内容
【题目】已知![]() ,
,![]() 平分
平分![]() .
.
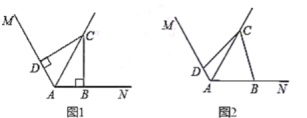
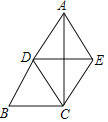
(1)在图1中![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
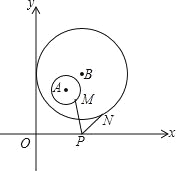
(2)在图2中![]() ,若
,若![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,见解析
【解析】
(1)根据含30°角的直角三角形的性质进行证明;
(2)作CE⊥AM、CF⊥AN于E、F.根据角平分线的性质,得CE=CF,根据等角的补角相等,得∠CDE=∠ABC,再根据AAS得到△CDE≌△CBF,则DE=BF.再由∠MAN=120°,AC平分∠MAN,得到∠ECA=∠FCA=30°,从而根据30°所对的直角边等于斜边的一半,得到AE=![]() AC,AF=
AC,AF=![]() AC,等量代换后即可证明AD+AB=AC仍成立.
AC,等量代换后即可证明AD+AB=AC仍成立.
(1)证明:∵∠MAN=120°,AC平分∠MAN,
∴∠CAD=∠CAB=60°.
又∠ABC=∠ADC=90°,
∴AD=![]() AC,AB=
AC,AB=![]() AC,
AC,
∴AB+AD=AC;
(2)解:结论仍成立.
理由如下:
作CE⊥AM、CF⊥AN于E、F.
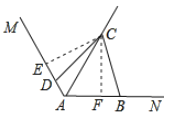
则∠CED=∠CFB=90°,
∵AC平分∠MAN,
∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°
∴∠CDE=∠ABC,
在△CDE和△CBF中,
 ,
,
∴△CDE≌△CBF(AAS),
∴DE=BF.
∵∠MAN=120°,AC平分∠MAN,
∴∠MAC=∠NAC=60°,
∴∠ECA=∠FCA=30°,
在Rt△ACE与Rt△ACF中,
则有AE=![]() AC,AF=
AC,AF=![]() AC,
AC,
则AD+AB
=AD+AF+BF
=AD+AF+DE
=AE+AF
=![]() AC+
AC+![]() AC
AC
=AC.
∴AD+AB=AC.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目