题目内容
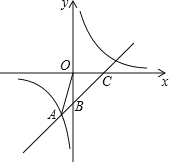
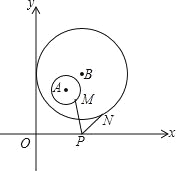
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
【答案】5![]() -4.
-4.
【解析】
试题作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到+PN的最小值.
试题解析:作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
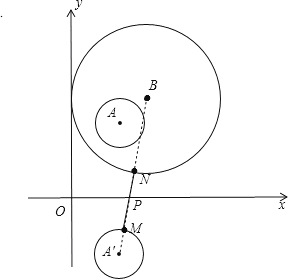
则此时PM+PN最小,
∵点A坐标(2,3),
∴点A′坐标(2,-3),
∵点B(3,4),
∴A′B=![]() ,
,
∴MN=A′B-BN-A′M=5![]() -3-1=5
-3-1=5![]() -4,
-4,
∴PM+PN的最小值为5![]() -4.
-4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目