题目内容
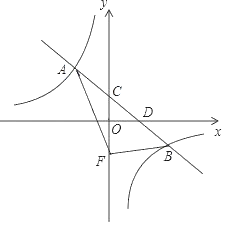
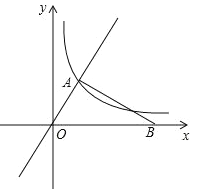
【题目】如图,在平面直角坐标系xOy中,已知直线![]() 与反比例函数
与反比例函数![]() (k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在∠AOB的内部求作点P,使点P到∠AOB的两边OA、OB的距离相等,且PA=PB;再写出点P的坐标.(不写作法,保留作图痕迹,在图上标注清楚点P)
【答案】(1)![]() ;(2)(4,0);(3)作图见解析,P(3,
;(2)(4,0);(3)作图见解析,P(3,![]() ).
).
【解析】
(1)利用待定系数法先求出点A纵坐标,再求出反比例系数k即可.
(2)过点A作AC⊥OB⊥,垂足为点C.在Rt△AOC中先求出OA,再在Rt△AOB中求出OB即可解决问题.
(3)画出∠AOB的平分线OM,线段AB的垂直平分线EF,OM与EF的交点就是所求的点P,设点P(m,![]() m),根据PA2=PB2,列出方程即可解决问题.
m),根据PA2=PB2,列出方程即可解决问题.
(1)由题意,设点A的坐标为(1,m).
∵点A在正比例函数y![]() x的图象上,∴m
x的图象上,∴m![]() .∴点A的坐标(1,
.∴点A的坐标(1,![]() ).
).
∵点A在反比例函数y![]() 的图象上,∴
的图象上,∴![]() ,解得:k
,解得:k![]() ,∴反比例函数的解析式为y
,∴反比例函数的解析式为y![]() .
.
(2)过点A作AC⊥OB于C,可得:OC=1,AC![]() .
.
∵AC⊥OB,∴∠ACO=90°.
由勾股定理,得:AO=2,∴OC![]() AO,∴∠OAC=30°,∴∠AOC=60°.
AO,∴∠OAC=30°,∴∠AOC=60°.
∵AB⊥OA,∴∠OAB=90°,∴∠ABO=30°,∴OB=2OA,∴OB=4,∴点B的坐标是(4,0).
(3)如图,作∠AOB的平分线OM,AB的垂直平分线EF,OM与EF的交点就是所求的点P.
∵∠POB=30°,∴可以设点P坐标(m,![]() m).
m).
∵PA2=PB2,∴(m﹣1)2+(![]() )2=(m﹣4)2+(
)2=(m﹣4)2+(![]() m)2,解得:m=3,∴点P的坐标是(3,
m)2,解得:m=3,∴点P的坐标是(3,![]() ).
).

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】某射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了8次测试,测试成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 10 | 8 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | 8 | 10 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙两名运动员8次测试成绩的方差;
(3)根据(1)(2)计算的结果,你认为推荐谁参加全国比赛更合适,并说明理由.