题目内容
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
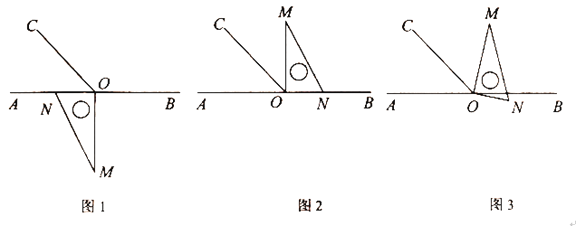
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;(2)点M的坐标为(2,0);(3)F1(﹣6,0),F2(2,0),F3(8﹣2
x﹣4;(2)点M的坐标为(2,0);(3)F1(﹣6,0),F2(2,0),F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0).
,0).
【解析】试题分析:(1)根据一元二次方程解法得出A,B两点的坐标,再利用交点式求出二次函数解析式;
(2)首先判定△MNA∽△BCA.得出![]() ,进而得出函数的最值;
,进而得出函数的最值;
(3)分别根据当AF为平行四边形的边时,AF平行且等于DE与当AF为平行四边形的对角线时,分析得出符合要求的答案.
试题解析:(1)∵x2﹣4x﹣12=0,
∴x1=﹣2,x2=6.
∴A(﹣2,0),B(6,0),
又∵抛物线过点A、B、C,故设抛物线的解析式为y=a(x+2)(x﹣6),
将点C的坐标代入,求得a=![]() ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣4;
x﹣4;
(2)设点M的坐标为(m,0),过点N作NH⊥x轴于点H(如图(1)).
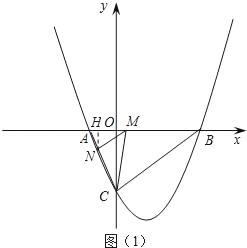
∵点A的坐标为(﹣2,0),点B的坐标为(6,0),
∴AB=8,AM=m+2,
∵MN∥BC,
∴△MNA∽△BCA.
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴NH=![]() ,
,
∴S△CMN=S△ACM﹣S△AMN=![]() AMCO﹣
AMCO﹣![]() AMNH,
AMNH,
=![]() m+2)(4﹣
m+2)(4﹣![]() )=﹣
)=﹣![]() m2+m+3,
m2+m+3,
=﹣![]() (m﹣2)2+4.
(m﹣2)2+4.
∴当m=2时,S△CMN有最大值4.
此时,点M的坐标为(2,0);
(3)∵点D(4,k)在抛物线y=![]() x2﹣
x2﹣![]() x﹣4上,
x﹣4上,
∴当x=4时,k=﹣4,
∴点D的坐标是(4,﹣4).
①如图(2),当AF为平行四边形的边时,AF平行且等于DE,
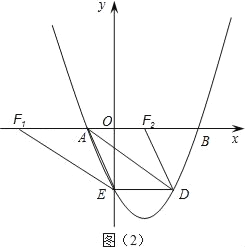
∵D(4,﹣4),
∴DE=4.
∴F1(﹣6,0),F2(2,0),
②如图(3),当AF为平行四边形的对角线时,设F(n,0),
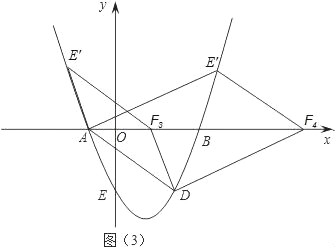
∵点A的坐标为(﹣2,0),
则平行四边形的对称中心的横坐标为:![]() ,
,
∴平行四边形的对称中心坐标为(![]() ,0),
,0),
∵D(4,﹣4),
∴E'的横坐标为:![]() ﹣4+
﹣4+![]() =n﹣6,
=n﹣6,
E'的纵坐标为:4,
∴E'的坐标为(n﹣6,4).
把E'(n﹣6,4)代入y=![]() x2﹣
x2﹣![]() x﹣4,得n2﹣16n+36=0.
x﹣4,得n2﹣16n+36=0.
解得n=8±2![]() .F3(8﹣2
.F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0),
,0),
综上所述F1(﹣6,0),F2(2,0),F3(8﹣2![]() ,0),F4(8+2
,0),F4(8+2![]() ,0).
,0).

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】铜仁某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:

![]() 根据图6提供的信息填写下表:
根据图6提供的信息填写下表:
平均数 | 众数 | 方差 | |
甲 |
| ||
乙 |
|
![]() 如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.