题目内容
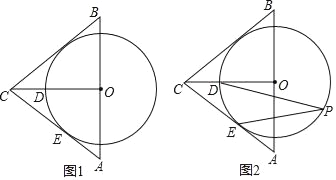
【题目】如图,在△ABC中,AC=CB,O是AB的中点,CA与⊙O相切于点E,CO交⊙O于点D
(1)求证:CB是⊙O的切线;
(2)若∠ACB=80°,点P是⊙O上一个动点(不与D,E两点重合),求∠DPE的度数.
【答案】(1)详见解析;(2)∠DPE的度数为25°或155°.
【解析】
(1)经过半径的外端且垂直于这条半径的直线是圆的切线,据此进行判断.
(2)依据∠ACB=80°,OC平分∠ACB,可得∠ACO=40°,∠DOE=90°-40°=50°,分两种情况:当点P在优弧弧DPE上时,∠DPE=![]() ∠DOE=25°;当点P在劣弧弧DE上时,∠DPE=180°-25°=155°.
∠DOE=25°;当点P在劣弧弧DE上时,∠DPE=180°-25°=155°.
解:(1)如图1所示,连接OE,过O作OF⊥BC于F,
∵CA与⊙O相切于点E,
∴OE⊥AC,
∵△ABC中,AC=CB,O是AB的中点,
∴OC平分∠ACB,
∴OE=OF,
又∵OE是⊙O的半径,
∴CB是⊙O的切线;
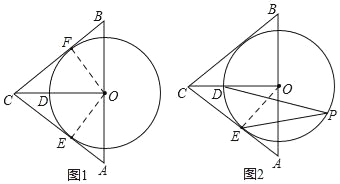
(2)如图2,∵∠ACB=80°,OC平分∠ACB,
∴∠ACO=40°,
又∵OE⊥AC,
∴∠DOE=90°﹣40°=50°,
当点P在优弧![]() 上时,∠DPE=
上时,∠DPE=![]() ∠DOE=25°;
∠DOE=25°;
当点P在劣弧![]() 上时,∠DPE=180°﹣25°=155°.
上时,∠DPE=180°﹣25°=155°.
∴∠DPE的度数为25°或155°.

练习册系列答案
相关题目