Question

已知：△ABC中，AB=AC，AD⊥BC于D．
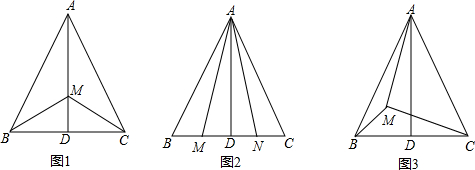
（1）如图（1），若点M在线段AD上（点M不与点A重合），则∠AMB______∠AMC（请填＞，=或＜）；
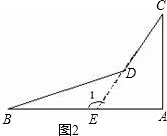
（2）如图2，若点M在线段BD上（点M不与点B，D重合），点N在线段CD上且ND=MD，则∠AMB______∠ANC，∠AMC______∠ANC（请填＞，=或＜）；
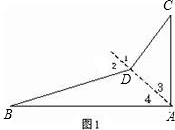
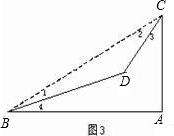
（3）如图3，若点M在△ABD的内部，是比较∠AMB与∠AMC的大小，并证明你的结论．

Answer 1

（1）∵AB=AC，AD⊥BC于D，
∴∠BAM=∠CAM（等腰三角形三线合一），
在△ABM与△ACM中，

AB=AC ∠BAM=∠CAM AM=AM

，
∴△ABM≌△ACM（SAS），
∴∠AMB=∠AMC；

（2）∵AD⊥BC，
∴∠ADM=∠ADN=90°，
在△ADM与△ADN中，

ND=MD ∠ADM=∠ADN=90° AD=AD

，
∴△ADM≌△ADN（SAS），
∴∠AMD=∠AND，
∴180°-∠AMD=180°-∠AND，
即∠AMB=∠ANC，
在Rt△ADN中，∠AND是锐角，
∴∠AND＜∠ANC，
∴∠AMC＜∠ANC；

（3）如图，作点M关于AD的对称点N，连接AN，CN，延长CN交AM于点P，
∵AB=AC，AD⊥BC于D，
∴AD垂直平分BC，
∴点B、C关于AD所在的直线对称，
∴△ABM≌△ACN，
∴∠1=∠2，
∵∠2是△APN的外角，
∴∠2＞∠3，
∵∠3是△PMC的外角，
∴∠3＞∠PMC，
∴∠1＞∠PMC，
即∠AMB＞∠AMC．
故答案为：（1）=；（2）=，＜；（3）∠AMB＞∠AMC．