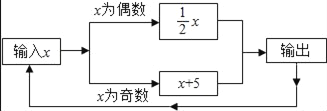
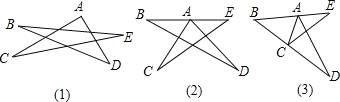
题目内容
【题目】在△ABC中，CA=CB=4，∠ACB=120°，将一块足够大的直角三角尺PMN（∠M=90°、∠MPN=30°）按如图所示放置，顶点P在线段AB上滑动，三角尺的直角边PM始终经过点C，并且与CB的夹角∠PCB=α，斜边PN交AC于点D．
（1）当PN∥BC时，∠ACP=_____度．
（2）在点P滑动的过程中，当AP长度为多少时，△ADP与△BPC全等．
（3）在点P的滑动过程中，△PCD的形状可以是等腰三角形吗？若不可以，请说明理由；若可以，请求出夹角α的大小．
【答案】90
【解析】
(1)当
∥
时，
，则
；(2)根据
，
，可得
，再根据外角的性质可得
，又
，可证
，即可得出结论.(3)在点P的滑动过程中，
的形状可以是等腰三角形，分三种情况考虑：当
；
；
，分别求出夹角
的大小即可.
(1)当∥时，
，
又∵，
∴
，
故答案为：
；
(2)当
时，，
理由为：∵，，
∴，
又∵
是
的一个外角，
∴
，
∵
，
∴，
又∵
时，
∴
；
(3)的形状可以是等腰三角形，
则
，
，
①当时，是等腰三角形，
∴
，即
，
∴
；
②当时，是等腰三角形，
∴
，即
，
∴
；
③当时，是等腰三角形，
∴
，
∴
，
即
，
∴
，
此时点P与点B重合，点D和A重合，
综合所述：当
或或
时，是等腰三角形．
练习册系列答案
备战中考寒假系列答案
相关题目
