题目内容
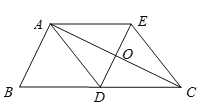
【题目】如图，已知△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，联结EC.
（1）求证：四边形ADCE是平行四边形；
（2）当∠BAC=90°时，求证：四边形ADCE是菱形.
【答案】证明见解析
【解析】分析：（1）先证四边形ABDE是平行四边形，再证四边形ADCE是平行四边形即可；
（2）由∠BAC=90°，AD是边BC上的中线，得AD=BD=CD，即可证明.
详解：(1)证明：∵AE∥BC，DE∥AB ，
∴四边形ABDE是平行四边形，
∴AE=BD，
∵AD是边BC上的中线，
∴BD=DC，
∴AE=DC，
又∵AE∥BC，
∴四边形ADCE是平行四边形.
(2) 证明：∵∠BAC=90°，AD是边BC上的中线.
∴AD=CD
∵四边形ADCE是平行四边形，
∴四边形ADCE是菱形.
练习册系列答案
名校课堂系列答案
相关题目
