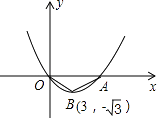题目内容
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

【答案】(1)证明见解析(2)![]()
【解析】分析:(1)由矩形ABCD中,O为BD的中点,易证得△PDO≌△QBO(ASA),继而证得OP=OQ;(2)AD=8cm,AP=tcm,即可用t表示PD的长;
(3)由四边形PBQD是菱形,可得PB=PD,即可得AB+AP=PD,继而可得方程6+t=(8-t),解此方程即可求得答案
本题解析:.
解:(1)∵四边形ABCD是矩形,∴AD∥BC,
∴∠PDO=∠QBO,∵O为BD的中点,∴DO=BO,
在△PDO和△QBO中,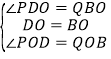
∴△PDO≌△QBO(ASA),∴OP=OQ;
(2)由题意知:AD=8cm,AP=tcm,∴PD=8﹣t,
(3)∵PB=PD,∴PB2=PD2,即AB2+AP2=PD2,
∴62+t2=(8-t)2,解得 t=![]() ,
,
∴当t=![]() 时,PB=PD.
时,PB=PD.

练习册系列答案
相关题目