Question

【题目】已知在中，．在边上取一点，以为顶点、为一条边作，点在的延长线上，．

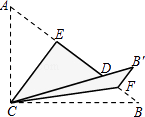
（1）如图（1），当点在边上时，请说明①；②成立的理由．

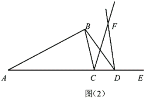
（2）如图（2），当点在的延长线上时，试判断与是否相等？

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）①直接利用三角形的外角性质，即可得到；

②过D作交于点，由等腰三角形的性质，平行线的性质和等边对等角，得到，，然后证明三角形全等，即可得到结论成立；

（2）连接BF，根据题意，可证得，则B、C、D、F四点共圆，即可证明结论成立.

解：（1）①∵，

即，

∵，

∴；

②过D作交于点，

∴，，

又，

∴，

∴，

∴，

∴，

∴，

又，

∴，

在与中，

∴

∴；

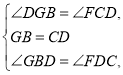
（2）证明：如图：连接BF，

由（1）可知，，

∵，

∴，

∵，

∴，

∴，

∴B、C、D、F四点共圆，

∴，，

∴，

∵，

∴，

∴.