题目内容
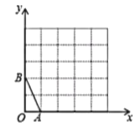
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣1,1)、B(0,﹣2)、C(1,0),点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得到点P2,点P2绕点C旋转180°得到点P3,
(1)在图中画出点P1、P2、P3;
(2)继续将点P3绕点A旋转180°得到点P4,点P4绕点B旋转180°得到点P5,…,按此作法进行下去,则点P2020的坐标为 .
【答案】(1)见解析;(2) (﹣2,﹣2)
【解析】
(1)利用网格特点和旋转的性质画出点P1、P2、P3即可;
(2)画出P1~P6,寻找规律后即可解决问题.
解:(1)点P1、P2、P3如图所示,
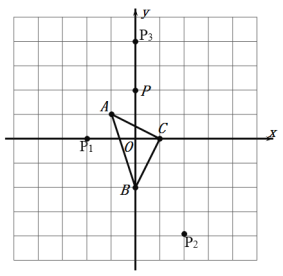
(2)(﹣2,﹣2)
解析:
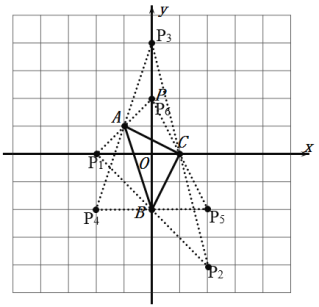
如图所示:P1(﹣2,0),P2(2,﹣4),P3(0,4),P4(﹣2,﹣2)P5(2,﹣2),P6(0,2)
∵6次一个循环
∴2020 ÷ 6 = 336... 4
∴P2020(﹣2,﹣2)

练习册系列答案
相关题目