题目内容
【题目】如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°. 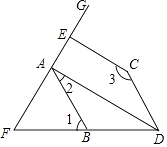
(1)请你判断∠1与∠BDC的数量关系,并说明理由;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
【答案】
(1)猜想:∠1=∠BDC
证明:∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°
∴AD∥CE
∴∠ADC+∠3=180°
又∵∠2+∠3=180°,
∴∠2=∠ADC
∴AB∥CD
∴∠1=∠BDC
(2)解:解:∵AD⊥EF,
∴∠FAD=90°.
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC= ![]() ∠BDC=
∠BDC= ![]() ×70°=35°.
×70°=35°.
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD﹣∠2=90°﹣35°=55°
【解析】(1)先根据垂直的定义得出∠GAD=∠GEC=90°,故可得出AD∥CE,再由平行线的性质∠ADC+∠3=180°,据此可得出AB∥CD,进而可得出结论;(2)先根据平行线的性质得出∠BDC=∠1=70°,再由DA平分∠BDC得出∠ADC的度数,进而得出∠2的度数,由∠FAB=∠FAD﹣∠2即可得出结论.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目