题目内容
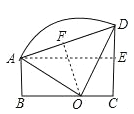
【题目】如图,梯形![]() 中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且
中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且![]() ,圆心O到弦AD的距离是____cm.
,圆心O到弦AD的距离是____cm.

【答案】![]() .
.
【解析】试题分析:如图,作AE⊥CD,垂足为E,OF⊥AD,垂足为F,
则四边形AECB是矩形,
CE=AB=2cm,DE=CD﹣CE=4﹣2=2cm,
∵∠AOD=90°,AO=OD,
所以△AOD是等腰直角三角形,
AO=OD,∠OAD=∠ADO=45°,BO=CD,
∵AB∥CD,
∴∠BAD+∠ADC=180°
∴∠ODC+∠OAB=90°,
∵∠ODC+∠DOC=90°,
∴∠DOC=∠BAO,
∵∠B=∠C=90°
∴△ABO≌△OCD,
∴OC=AB=2cm,OB=CD=4cm,BC=BO+OC=AE=6cm,
由勾股定理知,AD2=AE2+DE2,
得AD=2![]() cm,
cm,
∴AO=OD=2![]() cm,
cm,
S△AOD=![]() AODO=
AODO=![]() ADOF,
ADOF,
∴OF=![]() cm.
cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目