Question

【题目】已知：在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过点A（3，0），B（2，﹣3），C（0，﹣3）

（1）求抛物线的表达式；

（2）设点D是抛物线上一点，且点D的横坐标为﹣2，求△AOD的面积．

Answer 1

【答案】（1）y=x2﹣2x﹣3；（2）．

【解析】

试题分析：（1）把A，B，C三点坐标代入解析式求出a，b，c的值，即可求出函数解析式；

（2）把x=﹣2代入抛物线解析式求出y的值，确定出D坐标，由OA为底，D纵坐标绝对值为高，求出三角形AOD面积即可．

试题解析：（1）把A（3，0），B（2，﹣3），C（0，﹣3）代入y=ax2+bx+c得：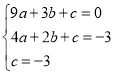

，解得：，则抛物线解析式为y=x2﹣2x﹣3；

（2）把x=﹣2代入抛物线解析式得：y=5，即D（﹣2，5），∵A（3，0），即OA=3，∴S△AOD=×3×5=．