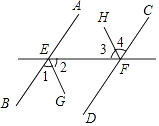题目内容
【题目】直线AB∥CD,E为直线AB、CD之间的一点.
(1)如图1,若∠B=15°,∠BED=90°,则∠D=°;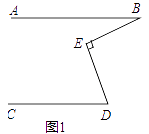
(2)如图2,若∠B=α,∠D=β,则∠BED=;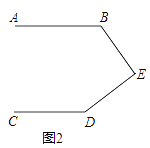
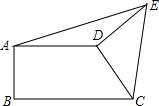
(3)如图3,若∠B=α,∠C=β,则α、β与∠BEC之间有什么等量关系?请猜想证明.
【答案】
(1)75°
(2)360°﹣α﹣β
(3)
猜想:∠BED=180°﹣α+β.
证明:过点E作EF∥AB,
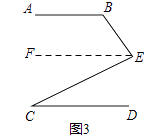
则∠BEF=180°﹣∠B=180°﹣α,
∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠CEF=∠C=β,
∴∠BEC=∠BEF+∠CEF=180°﹣α+β
【解析】解:(1.)过E作EF∥AB,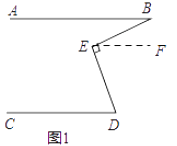
∵AB∥CD,
∴EF∥CD,
∵∠B=15°,
∴∠BEF=15°,
又∵∠BED=90°,
∴∠DEF=75°,
∵EF∥CD,
∴∠D=75°,
所以答案是:75°;
(2.)过E作EF∥AB,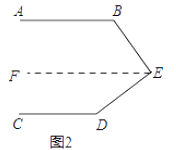
∵AB∥CD,
∴EF∥CD,
∴∠B+∠BEF+∠DEF+∠D=360°,
又∵∠B=α,∠D=β,
∴∠BED=∠BEF+∠DEF=360°﹣α﹣β,
所以答案是:∠BED=360°﹣α﹣β;
【考点精析】掌握平行线的性质是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目