题目内容
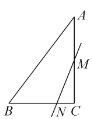
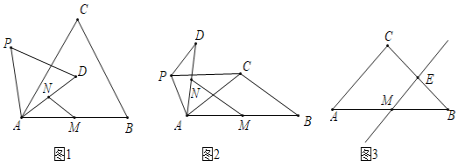
【题目】在△ABC中,CA=CB,∠ACB=α(0°<α<180°).点P是平面内不与A,C重合的任意一点,连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,CP.点M是AB的中点,点N是AD的中点.
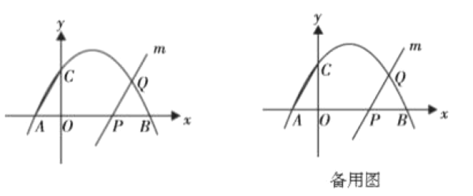
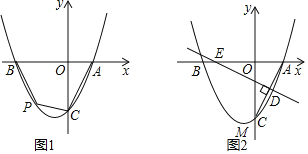
(1)问题发现:如图1,当α=60°时,![]() 的值是 ,直线MN与直线PC相交所成的较小角的度数是 .
的值是 ,直线MN与直线PC相交所成的较小角的度数是 .
(2)类比探究:如图2,当α=120°时,请写出的![]() 值及直线MN与直线PC相交所成的较小角的度数,并就图2的情形说明理由.
值及直线MN与直线PC相交所成的较小角的度数,并就图2的情形说明理由.
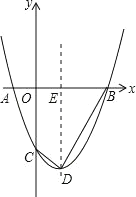
(3)解决问题:如图3,当α=90°时,若点E是CB的中点,点P在直线ME上,请直接写出点B,P,D在同一条直线上时![]() 的值.
的值.
【答案】(1)![]() ,60°;(2)
,60°;(2)![]() ,30°,见解析;(3)当点P在线段BD上时,
,30°,见解析;(3)当点P在线段BD上时, ![]() ,当点P在DB延长线上时,
,当点P在DB延长线上时,![]() =2+
=2+![]() .
.
【解析】
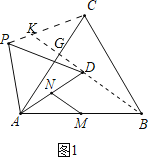
(1)如图1中,连接PC,BD,延长BD交PC于K,交AC于G.证明△PAC≌△DAB(SAS),利用全等三角形的性质以及三角形的中位线定理即可解决问题.
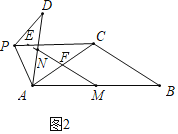
(2)如图设MN交AC于F,延长MN交PC于E.证明△ACP∽△AMN,推出∠ACP=∠AMN,![]() 可得结论.
可得结论.
(3)分两种情形分别画出图形,利用三角形中位线定理即可解决问题.
解:(1)如图1中,连接PC,BD,延长BD交PC于K,交AC于G.
∵CA=CB,∠ACB=60°,
∴△ABC是等边三角形,
∴∠CAB=∠PAD=60°,AC=AB,
∴∠PAC=∠DAB,
∵AP=AD,
∴△PAC≌△DAB(SAS),
∴PC=BD,∠ACP=∠ABD,
∵AN=ND,AM=BM,
∴BD=2MN,
∴![]() .
.
∵∠CGK=∠BGA,∠GCK=∠GBA,
∴∠CKG=∠BAG=60°,
∴BK与PC的较小的夹角为60°,
∵MN∥BK,
∴MN与PC较小的夹角为60°.
故答案为![]() ,60°.
,60°.
(2)如图设MN交AC于F,延长MN交PC于E.
∵CA=CB,PA=PD,∠APD=∠ACB=120°,
∴△PAD∽△CAB,
∴![]() ,
,
∵AM=MB,AN=ND,
∴![]() ,
,
∴△ACP∽△AMN,
∴∠ACP=∠AMN, ![]() ,
,
∵∠CFE=∠AFM,
∴∠FEC=∠FAM=30°.
(3)设MN=a,由(2)得![]() ,
,
∵∠ACB=90°,△ABC为等腰直角三角形,
∴AC=![]() AM
AM
∴![]() ,
,
∴PC=![]() a,
a,
∵ME是△ABC的中位线,∠ACB=90°,
∴ME是线段BC的中垂线,
∴PB=PC=![]() a,
a,
∵MN是△ADB的中位线,
∴DB=2MN=2a,
如图3﹣1中,当点P在线段BD上时,PD=DB﹣PB=(2﹣![]() )a,
)a,
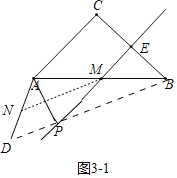
∴![]() .
.
如图3﹣2中,当点P在DB延长线上时,PD=DB+PB=(2+![]() )a,
)a,
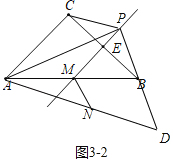
∴![]() =2+
=2+![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】某中学为了了解“校园文明监督岗”的值围情况,对全校各班级进行了抽样调查,过程如下:
收集数据:从三个年级中随机抽取了20个班级,学校对各班的评分如下:
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述数据:按如下分数段整理、描述这两组样本数据:
分数段 |
|
|
|
|
|
班级数 | 1 | 2 | a | 8 | b |
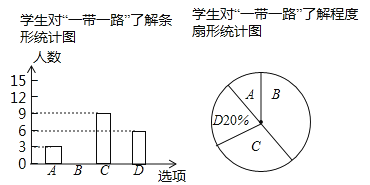
![]() 说明:成绩90分及以上为优秀,
说明:成绩90分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格
分为合格,60分以下为不合格![]()
分析数据:样本数据的平均数、中位数、众数、极差如下表,绘制扇形统计图:
平均数 | 中位数 | 众数 | 极差 |
79 | c | 82 | d |
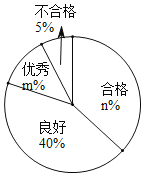
请根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 若我校共120个班级,估计得分为优秀的班级有多少个?
若我校共120个班级,估计得分为优秀的班级有多少个?
![]() 为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励
为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励![]() 如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由
如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由