题目内容
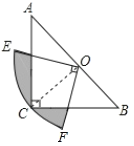
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
【答案】![]()
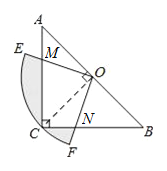
【解析】证明△AMO≌△CNO,将四边形CMON的面积转化为△ACO的面积,即可用割补法求出阴影部分的面积.
因为点O是AB的中点,所以AO=BO=CO,
由勾股定理得AB=![]() .
.
因为∠ACB=90°,∠EOF=90°,所以∠CMO+∠CNO=180°,又∠AMO+∠CMO=180°,所以∠AMO=∠CNO,
又因为∠A=∠B,AO=CO,
所以△AMO≌△CNO.
所以四边形CMON的面积=△CMO的面积+△CNO的面积
=△CMO的面积+△CNO的面积=△ACO的面积=△ABC面积的一半.
所以阴影部分的面积=扇形OEF的面积-四边形CMON的面积
=扇形OEF的面积-△ACO的面积
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目