��Ŀ����
����Ŀ������̽����
��ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
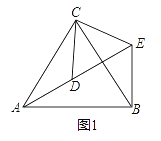
��1��֤����AD=BE��
��2�����AEB�Ķ�����
�����ʽ��
��3����ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE���������������AEB�Ķ������������ж��߶�CM��AE��BE֮���������ϵ����˵�����ɣ�
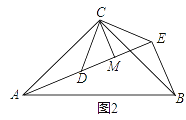
���𰸡���1������⣻��2��60������3��������90����������AE=BE+2CM�����ɼ����.
��������
��1����������ACB�͡�DCE��Ϊ�ȱ������Σ���֤��ACD�ա�BCE���Ӷ��õ���Ӧ����ȣ���AD=BE��
��2�����ݡ�ACD�ա�BCE���ɵá�ADC=��BEC���ɵ�A��D��E��ͬһֱ���ϣ��������ADC=120�����Ӷ����������AEB�Ķ�����
��3�����������ȸ��ݡ�ACB�͡�DCE��Ϊ����ֱ�������Σ��ɵ�AC=BC��CD=CE����ACB=��DCE=90�����ݴ��жϳ���ACD=��BCE��Ȼ�����ȫ�������ε��ж��������жϳ���ACD�ա�BCE�������жϳ�BE=AD����BEC=��ADC�������жϳ���AEB�Ķ���Ϊ90��������������DCE=90����CD=CE��CM��DE���ɵ�CM=DM=EM������DE=DM+EM=2CM���ݴ��жϳ�AE=BE+2CM��
�⣺��1����ͼ1��

�ߡ�ACB����DCE��Ϊ�ȱ������Σ�
��CA=CB��CD=CE����ACB=��DCE=60����
���ACD=��BCE��
����ACD����BCE��
���ACD�ա�BCE��SAS����
��AD=BE��
��2����ͼ1���ߡ�ACD�ա�BCE��
���ADC=��BEC��
�ߡ�DCEΪ�ȱ������Σ�
���CDE=��CED=60����
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=120����
���BEC=120����
���AEB=��BEC-��CED=60����
��3����������ͼ2��
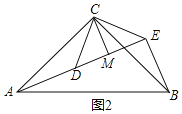
�ߡ�ACB����DCE��Ϊ����ֱ�������Σ�
��AC=BC��CD=CE����ACB=��DCE=90������CDE=��CED=45����
���ACB-��DCB=��DCE-��DCB��
����ACD=��BCE��
����ACD����BCE�� ��
��
���ACD�ա�BCE��SAS����
��BE=AD����BEC=��ADC��
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=180-45=135����
���BEC=135����
���AEB=��BEC-��CED=135��-45��=90����
�ʴ�Ϊ��90����
��������ͼ2���ߡ�DCE=90����CD=CE��CM��DE��
��CM=DM=EM��
��DE=DM+EM=2CM��
�ߡ�ACD�ա�BCE����֤����
��BE=AD��
��AE=AD+DE=BE+2CM��
�ʴ�Ϊ��AE=BE+2CM��

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�