Question

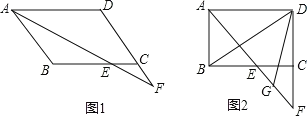
【题目】如图在RtΔABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过O作OE∥AB，交BC于E．

（1）求证：ED是⊙O的切线；

（2）如果⊙O的半径为1.5，ED=2，求AB的长．

（3）在（2）的条件下，求△ADO的面积．

Answer 1

【答案】（1）答案见解析；（2）5；（3）1.08．

【解析】

（1）连OD，首先证明△EOC≌△EOD，则可以证得∠EDO=∠ECO=90°，即可证得；

（2）证明OE是△ABC的中位线，在直角△OEC中，利用勾股定理求得OE的长，然后利用三角形中位线定理求得AB的长；

（3）连接CD，则CD是直角△ABC的斜边AB上的高，根据三角形的面积公式即可求得CD的长，则在直角△ACD中，利用勾股定理求得AD的长，则可求出△ACD的面积，进而求得△ADO的面积．

（1）连OD．

∵OE∥AB，∴∠EOC=∠A，∠EOD=∠ODA．

又∵OA=OD，∴∠A=∠ODA，∴∠EOC=∠EOD．

在△EOC和△EOD中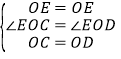，∵，∴△EOC≌△EOD（SAS），∴∠EDO=∠ECO．

又∵∠ECO=90°，∴∠EDO=90°即ED⊥DO 而点D在⊙O上，∴ED为⊙O的切线．

（2）∵OE∥AB，OA=OC，∴AB=2OE．

在△OCE中，OE= ，∴AB=2OE=5；

（3）连结CD．

∵AC=2OA=3，AB=5，∴BC===4．

∵AC是⊙O的直径，∴∠CDA=90°，∴CD⊥AB．

在Rt△ABC中，CD⊥AB，∴CDAB=ACBC，∴CD=2.4．

在Rt△ACD中，AD===1.8，∴S△ACD=CDAD=2.16，∴S△ADO=S△ACD=1.08．